
【题目】要在如图所示的花圃中的5个区域中种入4种颜色不同的花,要求相邻区域不同色,有种不同的种法(用数字作答). 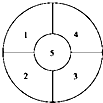
【答案】72
【解析】解:首先,区域1可取4种颜色任何一种色,有 ![]() 种,区域2只能取除1以外的颜色有
种,区域2只能取除1以外的颜色有 ![]() 种; 区域4与区域2不相邻,也可取除1以外的3种颜色,有
种; 区域4与区域2不相邻,也可取除1以外的3种颜色,有 ![]() 种;
种;
区域5有两种可能:①区域2,区域4取同一色,有 ![]() 种;②区域2,区域4取不同色,区域5只有一色可取,有
种;②区域2,区域4取不同色,区域5只有一色可取,有 ![]() 种方法;
种方法;
区域3也有2种可能:若区域2,区域4取同一色,有 ![]() 种取法;若区域2,区域4取不同色,区域5只有一色可取,有
种取法;若区域2,区域4取不同色,区域5只有一色可取,有 ![]() 种方法;
种方法;
区域2、区域4共 ![]() ×
× ![]() =3×3=9取法中,3种取法是同一色的,6种取法是不同色的;
=3×3=9取法中,3种取法是同一色的,6种取法是不同色的;
所以,共有着色方法 ![]() ×3×
×3× ![]() ×
× ![]() +
+ ![]() ×6×
×6× ![]() ×
× ![]()
=4×3×2×2+4×6×1×1
=48+24
=72种.
故答案为:72.
区域1可取4种颜色任何一种色,有 ![]() 种,区域2只能取除区域1以外的颜色有
种,区域2只能取除区域1以外的颜色有 ![]() 种,区域4与区域2不相邻,有
种,区域4与区域2不相邻,有 ![]() 种;再对区域5与区域3分类讨论,最后利用乘法原理与加法原理运算即可求得答案.
种;再对区域5与区域3分类讨论,最后利用乘法原理与加法原理运算即可求得答案.


科目:高中数学 来源: 题型:
【题目】已知数列{an}满足log3an+1=log3an+1(n∈N*),且a2+a4+a6=9,则 ![]() (a5+a7+a9)的值是( )
(a5+a7+a9)的值是( )
A.﹣5
B.- ![]()
C.5
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx,g(x)=x2 . (Ⅰ)求函数h(x)=f(x)﹣x+1的最大值;
(Ⅱ)对于任意x1 , x2∈(0,+∞),且x1<x2 , 是否存在实数m,使mg(x1)﹣mg(x2)﹣x2f(x2)+x1f(x1)恒为正数?若存在,求出m的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知结论:“在正三角形ABC中,若D是边BC的中点,G是三角形ABC的重心,则 ![]() ”,若把该结论推广到空间,则有结论:“在棱长都相等的四面体ABCD中,若△BCD的中心为M,四面体内部一点O到四面体各面的距离都相等,则
”,若把该结论推广到空间,则有结论:“在棱长都相等的四面体ABCD中,若△BCD的中心为M,四面体内部一点O到四面体各面的距离都相等,则 ![]() =( )
=( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥E﹣ABCD中,底面ABCD为正方形,EC⊥平面ABCD,AB= ![]() ,CE=1,G为AC与BD交点,F为EG中点, (Ⅰ)求证:CF⊥平面BDE;
,CE=1,G为AC与BD交点,F为EG中点, (Ⅰ)求证:CF⊥平面BDE;
(Ⅱ)求二面角A﹣BE﹣D的大小.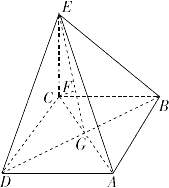
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】奇函数f(x)在(0,+∞)内单调递增且f(2)=0,则不等式 ![]() 的解集为( )
的解集为( )
A.(﹣∞,﹣2)∪(0,1)∪(1,2)
B.(﹣2,0)∪(1,2)
C.(﹣∞,﹣2)∪(2,+∞)
D.(﹣∞,﹣2)∪(0,1)∪(2,+∞)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com