
【题目】设函数![]() .
.
(1)求![]() 时,函数
时,函数![]() 的单调区间;
的单调区间;
(2)若函数![]() 有两个零点,求正整数
有两个零点,求正整数![]() 的最小值
的最小值
【答案】(1)函数![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() ;(2)3.
;(2)3.
【解析】
(1)当![]() 时,对
时,对![]() 进行求导得
进行求导得![]() ,根据导数研究函数的单调性,即可求出函数
,根据导数研究函数的单调性,即可求出函数![]() 的单调区间;
的单调区间;
(2)先求导得![]() ,分两种情况当
,分两种情况当![]() 和当
和当![]() 时,根据导数研究函数的单调性,讨论
时,根据导数研究函数的单调性,讨论![]() 的单调性,如果函数
的单调性,如果函数![]() 有两个零点,得出
有两个零点,得出![]() ,且
,且![]() ,即:
,即:![]() ,构造函数
,构造函数![]() ,求得
,求得![]() 在区间
在区间![]() 内为增函数,且
内为增函数,且![]() ,
,![]() ,存在
,存在![]() 进而得出答案.
进而得出答案.
解:(1)当![]() 时,得
时,得![]() ,则
,则![]() 的定义域为
的定义域为![]() ,
,
![]() ,
,
当![]() 时,即
时,即![]() ,解得:
,解得:![]() 或
或![]() (舍去),
(舍去),
令![]() ,解得:
,解得:![]() ,则
,则![]() 时,
时,![]() 单调递增;
单调递增;
令![]() ,解得:
,解得:![]() ,则
,则![]() 时,
时,![]() 单调递减,
单调递减,
综上得:函数![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() .
.
(2)由题可知,![]() ,则
,则![]() 的定义域为
的定义域为![]() ,
,
![]() ,
,
当![]() 时,
时,![]() ,函数
,函数![]() 在区间
在区间![]() 内单调递增,
内单调递增,
所以,函数![]() 的单调增区间为
的单调增区间为![]() ,无单调减区间;
,无单调减区间;
当![]() 时,由
时,由![]() ,得
,得![]() ;由
;由![]() ,得
,得![]() ,
,
所以,函数![]() 的单调增区间为
的单调增区间为![]() ,
,![]() ,单调减区间为
,单调减区间为![]() ,
,
如果函数![]() 有两个零点,则
有两个零点,则![]() ,且
,且![]() ,
,
即![]() ,即:
,即:![]() ,
,
令![]() ,则
,则![]() ,
,
可知![]() 在区间
在区间![]() 内为增函数,且
内为增函数,且![]() ,
,
![]() ,
,
所以存在![]() ,
,![]() ,
,
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,
,
所以,满足条件的最小正整数![]() .
.


 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:高中数学 来源: 题型:
【题目】若函数![]() 在其图象上存在不同的两点
在其图象上存在不同的两点![]() ,其坐标满足条件:
,其坐标满足条件:![]() 的最大值为0,则称
的最大值为0,则称![]() 为“柯西函数”,则下列函数:
为“柯西函数”,则下列函数:
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中是“柯西函数”的为( )
.其中是“柯西函数”的为( )
A.①②B.③④C.①③D.②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() ,其中
,其中![]() 为常数,函数
为常数,函数![]() 和
和![]() 的图象在它们与坐标轴交点处的切线互相平行.
的图象在它们与坐标轴交点处的切线互相平行.
(1)求![]() 的值;
的值;
(2)若存在![]() ,使不等式
,使不等式![]() 成立,求实数
成立,求实数![]() 的取值范围;
的取值范围;
(3)令![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设D是圆O:x2+y2=16上的任意一点,m是过点D且与x轴垂直的直线,E是直线m与x轴的交点,点Q在直线m上,且满足2|EQ|![]() |ED|.当点D在圆O上运动时,记点Q的轨迹为曲线C.
|ED|.当点D在圆O上运动时,记点Q的轨迹为曲线C.
(1)求曲线C的方程.
(2)已知点P(2,3),过F(2,0)的直线l交曲线C于A,B两点,交直线x=8于点M.判定直线PA,PM,PB的斜率是否依次构成等差数列?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
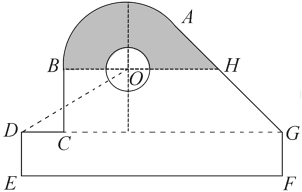
【题目】某中学开展劳动实习,学生加工制作零件,零件的截面如图所示.O为圆孔及轮廓圆弧AB所在圆的圆心,A是圆弧AB与直线AG的切点,B是圆弧AB与直线BC的切点,四边形DEFG为矩形,BC⊥DG,垂足为C,tan∠ODC=![]() ,
,![]() ,EF=12 cm,DE=2 cm,A到直线DE和EF的距离均为7 cm,圆孔半径为1 cm,则图中阴影部分的面积为________cm2.
,EF=12 cm,DE=2 cm,A到直线DE和EF的距离均为7 cm,圆孔半径为1 cm,则图中阴影部分的面积为________cm2.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() 的离心率为
的离心率为![]() ,且过点
,且过点![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设![]() 为椭圆
为椭圆![]() 上任一点,
上任一点, ![]() 为其右焦点,点
为其右焦点,点![]() 满足
满足![]() .
.
①证明: ![]() 为定值;
为定值;
②设直线![]() 与椭圆
与椭圆![]() 有两个不同的交点
有两个不同的交点![]() ,与
,与![]() 轴交于点
轴交于点![]() .若
.若![]() 成等差数列,求
成等差数列,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场为了了解顾客的购物信息,随机在商场收集了![]() 位顾客购物的相关数据如下表:
位顾客购物的相关数据如下表:
一次购物款(单位:元) |
|
|
|
|
|
顾客人数 |
|
|
|
|
|
统计结果显示![]() 位顾客中购物款不低于
位顾客中购物款不低于![]() 元的顾客占
元的顾客占![]() ,该商场每日大约有
,该商场每日大约有![]() 名顾客,为了增加商场销售额度,对一次购物不低于
名顾客,为了增加商场销售额度,对一次购物不低于![]() 元的顾客发放纪念品.
元的顾客发放纪念品.
(Ⅰ)试确定![]() ,
, ![]() 的值,并估计每日应准备纪念品的数量;
的值,并估计每日应准备纪念品的数量;
(Ⅱ)为了迎接春节,商场进行让利活动,一次购物款![]() 元及以上的一次返利
元及以上的一次返利![]() 元;一次购物不超过
元;一次购物不超过![]() 元的按购物款的百分比返利,具体见下表:
元的按购物款的百分比返利,具体见下表:
一次购物款(单位:元) |
|
|
|
|
返利百分比 |
|
|
|
|
请问该商场日均大约让利多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com