
分析 (Ⅰ)求出f(x)的定义域,以及导数,讨论a=0,a>0,a<0,判断导数符号,解不等式即可得到所求单调区间;
(Ⅱ)运用分析法证明.要证men+n<nem+m,即证men-m<nem-n,也就是证$\frac{{e}^{n}-1}{n}$<$\frac{{e}^{m}-1}{m}$,令g(x)=$\frac{{e}^{x}-1}{x}$,x>0,求出导数,再令h(x)=xex-ex+1,求出导数,判断单调性,即可得证.
解答 (Ⅰ)解:f(x)的定义域为R,且f′(x)=(ax+a-1)ex.
当a=0时,f′(x)=-ex<0,此时f(x)的单调递减区间为(-∞,+∞);
当a>0时,由f′(x)>0,得x>-$\frac{a-1}{a}$,由f′(x)<0,得x<-$\frac{a-1}{a}$.
此时f(x)的单调减区间为(-∞,-$\frac{a-1}{a}$),单调增区间为($-\frac{a-1}{a}$,+∞);
当a<0时,由f′(x)>0,得x<-$\frac{a-1}{a}$,由f′(x)<0,得x>-$\frac{a-1}{a}$.
此时f(x)的单调减区间为($-\frac{a-1}{a}$,+∞),单调增区间为(-∞,-$\frac{a-1}{a}$).
(Ⅱ)证明:要证men+n<nem+m,即证men-m<nem-n,
也就是证m(en-1)<n(em-1).
也就是证$\frac{{e}^{n}-1}{n}$<$\frac{{e}^{m}-1}{m}$,
令g(x)=$\frac{{e}^{x}-1}{x}$,x>0,g′(x)=$\frac{x{e}^{x}-{e}^{x}+1}{{x}^{2}}$,
再令h(x)=xex-ex+1,h′(x)=ex+xex-ex=xex>0,
可得h(x)在x>0递增,即有h(x)>h(0)=0,
则g′(x)>0,g(x)在(0,+∞)递增,
由m>n>0,可得$\frac{{e}^{n}-1}{n}$<$\frac{{e}^{m}-1}{m}$,
故原不等式成立.
点评 本题考查函数的单调性、导数及其应用、不等式的证明等基础知识,考查推理论证能力、运算求解能力及抽象概括能力,考查函数与方程思想、分类与整合思想,属难题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
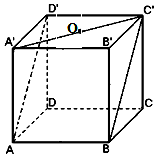
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{4}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
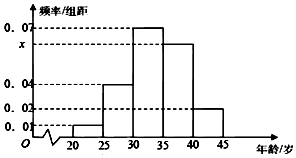 为增强市民的节能环保意识,郑州市面向全市征召义务宣传志愿者,从符合条件的500名志愿者中随机抽取100名,其年龄频率分布直方图如图所示,其中年龄分组区是:[20,25],[25,30],[30,35],[35,40],[40,45].
为增强市民的节能环保意识,郑州市面向全市征召义务宣传志愿者,从符合条件的500名志愿者中随机抽取100名,其年龄频率分布直方图如图所示,其中年龄分组区是:[20,25],[25,30],[30,35],[35,40],[40,45].查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 42 | B. | 44 | C. | 46 | D. | 48 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com