
【题目】超市为了防止转基因产品影响民众的身体健康,要求产品在进入超市前必须进行两轮转基因检测,只有两轮都合格才能销售,否则不能销售.已知某产品第一轮检测不合格的概率为![]() ,第二轮检测不合格的概率为
,第二轮检测不合格的概率为![]() ,两轮检测是否合格相互没有影响.
,两轮检测是否合格相互没有影响.
(1)求该产品不能销售的概率;
(2)如果产品可以销售,则每件产品可获利50元;如果产品不能销售,则每件产品亏损60元.已知一箱中有产品4件,记一箱产品获利![]() 元,求
元,求![]() 的分布列,并求出均值
的分布列,并求出均值![]() .
.
 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:高中数学 来源: 题型:
【题目】小王投资1万元2万元、3万元获得的收益分别是4万元、9万元、16万元为了预测投资资金x(万元)与收益y万元)之间的关系,小王选择了甲模型![]() 和乙模型
和乙模型![]() .
.
(1)根据小王选择的甲、乙两个模型,求实数a,b,c,p,q,r的值
(2)若小王投资4万元,获得收益是25.2万元,请问选择哪个模型较好?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】西北某省会城市计划新修一座城市运动公园,设计平面如图所示:其为五边形![]() ,其中三角形区域
,其中三角形区域![]() 为球类活动场所;四边形
为球类活动场所;四边形![]() 为文艺活动场所,
为文艺活动场所,![]() ,为运动小道(不考虑宽度)
,为运动小道(不考虑宽度)![]() ,
,![]() ,
,![]() 千米.
千米.

(1)求小道![]() 的长度;
的长度;
(2)求球类活动场所![]() 的面积最大值.
的面积最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有一块铁皮零件,其形状是由边长为![]() 的正方形截去一个三角形
的正方形截去一个三角形![]() 所得的五边形
所得的五边形![]() ,其中
,其中![]()
![]() ,如图所示.现在需要用这块材料截取矩形铁皮
,如图所示.现在需要用这块材料截取矩形铁皮![]() ,使得矩形相邻两边分别落在
,使得矩形相邻两边分别落在![]()
![]() 上,另一顶点
上,另一顶点![]() 落在边
落在边![]() 或
或![]() 边上.设
边上.设![]() ,矩形
,矩形![]() 的面积为
的面积为![]() .
.

(1)试求出矩形铁皮![]() 的面积
的面积![]() 关于
关于![]() 的函数解析式,并写出定义域;
的函数解析式,并写出定义域;
(2)试问如何截取(即![]() 取何值时),可使得到的矩形
取何值时),可使得到的矩形![]() 的面积最大?
的面积最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某圆柱的高为2,底面周长为16,其三视图如图所示,圆柱表面上的点![]() 在正视图上的对应点为
在正视图上的对应点为![]() ,圆柱表面上的点
,圆柱表面上的点![]() 在左视图上的对应点为
在左视图上的对应点为![]() ,则在此圆柱侧面上,从
,则在此圆柱侧面上,从![]() 到
到![]() 的路径中,最短路径的长度为( )
的路径中,最短路径的长度为( )

A. ![]() B.
B. ![]() C.
C. ![]() D. 2
D. 2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年是中国改革开放的第40周年,为了充分认识新形势下改革开放的时代性,某地的民调机构随机选取了该地的100名市民进行调查,将他们的年龄分成6段:![]() ,并绘制了如图所示的频率分布直方图.
,并绘制了如图所示的频率分布直方图.

(1)现从年龄在![]() 内的人员中按分层抽样的方法抽取8人,再从这8人中随机抽取3人进行座谈,用
内的人员中按分层抽样的方法抽取8人,再从这8人中随机抽取3人进行座谈,用![]() 表示年龄在
表示年龄在![]() 内的人数,求
内的人数,求![]() 的分布列和数学期望;
的分布列和数学期望;
(2)若用样本的频率代替概率,用随机抽样的方法从该地抽取20名市民进行调查,其中有![]() 名市民的年龄在
名市民的年龄在![]() 的概率为
的概率为![]() .当
.当![]() 最大时,求
最大时,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 是定义在
是定义在![]() 上的偶函数,当
上的偶函数,当![]() 时,
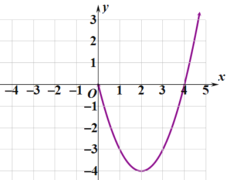
时,![]() .现已画出函数
.现已画出函数![]() 在
在![]() 轴右侧的图象,如图所示.
轴右侧的图象,如图所示.
(1)画出函数![]() 在
在![]() 轴左侧的图象,根据图象写出函数
轴左侧的图象,根据图象写出函数![]() 在
在![]() 上的单调区间;
上的单调区间;
(2)求函数![]() 在
在![]() 上的解析式;
上的解析式;
(3)解不等式![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com