
����Ŀ����ijѧУ�����꼶��800�������������ȡ50�˲������ߣ����ݱ���������ѧ������ȫ������155cm��195cm֮�䣬��������������·�ʽ�ֳɰ��飺��һ��[155��160�����ڶ���[160��165���������ڰ���[190��195]����ͼ�ǰ��������鷽���õ���Ƶ�ʷֲ�ֱ��ͼ��һ���֣���֪��һ����ڰ���������ͬ��������ȵ�������1�ˣ� 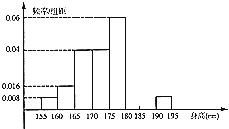
��1����������ѧУ�����꼶ȫ������������180cm���ϣ���180cm����������
��2�������������ڵ�����͵ڰ�������������������ȡ���ˣ������ǵ����߷ֱ�Ϊx��y�������㡰|x��y|��5�����¼��ĸ��ʣ�
���𰸡�
��1���⣺��Ƶ�ʷֲ�ֱ��ͼ��������180cm���ϣ���180cm��Ϊ������飬
���������Ƶ��Ϊ��0.016+0.012+0.008����5=0.18��
����ѧУ�����꼶ȫ������������180cm���ϣ���180cm��������Ϊ800��0.18=144
��2���⣺����֪��������[180��185���ڵ�����Ϊ4����Ϊa��b��c��d��
������[190��195]�ڵ�����Ϊ2����ΪA��B��
��x��y��[180��185��ʱ����ab��ac��ad��bc��bd��cd��6�������
��x��y��[190��195]ʱ����AB��1�������
��x��y�ֱ���[180��185����[190��195]��ʱ����aA��bA��cA��dA��aB��bB��cB��dB����8�������
���ԣ������¼�����Ϊ6+1+8=15��
�¼���|x��y|��5����ȡ��������ͬһ�飬���������Ļ����¼�������6+1=7��
����P��|x��y|��5��= ![]()
����������1����Ƶ�ʷֲ�ֱ��ͼ��������180cm���ϣ���180cm��Ϊ������飬����ɵ���������Ƶ�ʣ�����ȫУ������������������ɵø����꼶ȫ������������180cm������������2���������⣬�����ɵ�������[180��185���ڵ�����Ϊ4����Ϊa��b��c��d��������[190��195]�ڵ�����Ϊ2����ΪA��B�������оٴ�6����ȡ��2�˵�����������ɵû����¼��������¼���|x��y|��5���������Ļ����¼���Ŀ���ɹŵ����ʽ������ɵô�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����{an}����a1=1��an+1=2an��3����1��n��n��N*����
��1����bn=a2n��1����֤��bn+1=4bn��
��2��������{an}��ͨ�ʽ��
��3����a1+2a2+3a3+��+nan����2n��һ��������n���������ʵ���˵�ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() .
.
��I��������![]() �ϵ�
�ϵ�![]() �������߹���
�������߹���![]() ������
������![]() �ĵ��������䣻
�ĵ��������䣻
��II��������![]() ������
������![]() ������㣬��ʵ��
������㣬��ʵ��![]() ����Сֵ.
����Сֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��Ϊ�˽�ס������������������IJ�Ʒ�������������������������IJ�Ʒ�������ȡ��10����������Ʒ��ij��Ԫ�صĺ�������λ�����ˣ�����ͼ�Dz������ݵľ�Ҷͼ��
�涨������Ʒ�еĴ���Ԫ�غ��������18����ʱ���ò�ƷΪ�ŵ�Ʒ��
��1�������������ݣ�����ס������������߲�Ʒ�����ľ�ֵ�뷽���˵�����������ߵIJ�Ʒ����������ȶ���
��2�����ҳ����������10����Ʒ�У������ȡ3������鵽��3����Ʒ���ŵ�Ʒ���εķֲ��м�����ѧ����E���Σ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���躯��f��x��=x2+aln��x+1����
��1������f��x���ĵ������䣻
��2��������F��x��=f��x��+ln ![]() ��������ֵ��x1 �� x2��x1��x2 �� ��֤F��x2����
��������ֵ��x1 �� x2��x1��x2 �� ��֤F��x2���� ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=x�� ![]() ���ڵ����ݼ����䣬��y=f��x����ͼ����x=0��������l������y=ex���У��������������l�� ��
���ڵ����ݼ����䣬��y=f��x����ͼ����x=0��������l������y=ex���У��������������l�� ��
A.��3��
B.��2��
C.��1��
D.������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ֪��l��y=x+1��ԲO�� ![]() ��ֱ��l��Բ�صõ��ҳ�����ԲC��
��ֱ��l��Բ�صõ��ҳ�����ԲC�� ![]() �Ķ��᳤��ȣ���Բ��������e=
�Ķ��᳤��ȣ���Բ��������e= ![]() ��
��
��1������ԲC�ķ��̣�
��2������M��0�� ![]() ���Ķ�ֱ��l����ԲC��A��B���㣬���ʣ�������ƽ�����Ƿ����һ������T��ʹ������l���ת������ABΪֱ����Բ�������T�������ڣ������T�����ꣻ�������ڣ���˵�����ɣ�
���Ķ�ֱ��l����ԲC��A��B���㣬���ʣ�������ƽ�����Ƿ����һ������T��ʹ������l���ת������ABΪֱ����Բ�������T�������ڣ������T�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����{an}��ǰn���ΪSn �� a1= ![]() ���Ҷ�������������m��n����an+m=anam �� ��Sn��a������n��N*���������ʵ��a����Сֵ�� ��
���Ҷ�������������m��n����an+m=anam �� ��Sn��a������n��N*���������ʵ��a����Сֵ�� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ֵ.
��1����֪cos��= ![]() ����Ϊ��ǣ���tan2����ֵ��
����Ϊ��ǣ���tan2����ֵ��
��2����֪sin����+ ![]() ��=
��= ![]() ����Ϊ�۽ǣ���cos�ȵ�ֵ��
����Ϊ�۽ǣ���cos�ȵ�ֵ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com