
| A. | S2 | B. | 3S2 | C. | 9S2 | D. | 9S2-6S+1 |
分析 根据平均数与方差的定义,即可推导出结论.
解答 解:数据x1,x2,…xn的平均数为
$\overline{x}$=$\frac{1}{n}$(x1+x2+…+xn),
方差为S2=$\frac{1}{n}$[${{(x}_{1}-\overline{x})}^{2}$+${{(x}_{2}-\overline{x})}^{2}$+…+${{(x}_{n}-\overline{x})}^{2}$];
所以数据3x1-1,3x2-1,…3xn-1的平均数为
$\overline{x′}$=$\frac{1}{n}$[(3x1-1)+(3x2-1)+…+(3xn-1)]
=3•$\frac{1}{n}$(x1+x2+…+xn)-1
=3$\overline{x}$-1,
方差为s′2=$\frac{1}{n}$[${({3x}_{1}-1-3\overline{x}+1)}^{2}$+${({3x}_{2}-1-3\overline{x}+1)}^{2}$+…+${({3x}_{n}-1-3\overline{x}+1)}^{2}$]
=9•$\frac{1}{n}$[${{(x}_{1}-\overline{x})}^{2}$+${{(x}_{2}-\overline{x})}^{2}$+..${{(x}_{n}-\overline{x})}^{2}$]
=9s2.
故选:C.
点评 本题考查了平均数与方差的概念与计算问题,是基础题目.


科目:高中数学 来源: 题型:选择题
| A. | $2±\sqrt{2}$ | B. | $3±2\sqrt{2}$ | C. | $4±2\sqrt{3}$ | D. | $4±2\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{2}}{4}$ | B. | $\frac{1}{8}$ | C. | $\frac{1}{4}$ | D. | $\frac{\sqrt{2}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
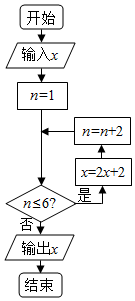
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{7}{30}$ | D. | $\frac{7}{8}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com