
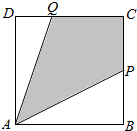
 如图,有一块边长为1(百米)的正方形区域ABCD.在点A处有一个可转动的探照灯,其照射角∠PAQ始终为45°(其中点P,Q分别在边BC,CD上),设BP=t.
如图,有一块边长为1(百米)的正方形区域ABCD.在点A处有一个可转动的探照灯,其照射角∠PAQ始终为45°(其中点P,Q分别在边BC,CD上),设BP=t.分析 (Ⅰ)由BP=t,得CP=1-t,0≤t≤1,设∠PAB=θ,则∠DAQ=45°-θ,分别求出CP,CQ,PQ即可得到求出周长l=2,问题得以解决;
(Ⅱ)根据S=S正方形ABCD-S△ABP-S△ADQ得到S=2-($\frac{t+1}{2}$+$\frac{1}{t+1}$),根据基本不等式的性质即可求出S的最大值.
解答 解:(Ⅰ)由BP=t,得CP=1-t,0≤t≤1,
设∠PAB=θ,
则∠DAQ=45°-θ,
DQ=tan(45°-θ)=$\frac{1-t}{1+t}$,CQ=1-$\frac{1-t}{1+t}$=$\frac{2t}{1+t}$,
∴PQ=$\sqrt{C{P}^{2}+C{Q}^{2}}$=$\sqrt{(1-t)^{2}+(\frac{2t}{1+t})^{2}}$=$\frac{1+{t}^{2}}{1+t}$,
∴l=CP+CQ+PQ=1-t+$\frac{2t}{1+t}$+$\frac{1+{t}^{2}}{1+t}$=1-t+1+t=2,是定值
(Ⅱ)S=S正方形ABCD-S△ABP-S△ADQ=1×1-$\frac{1}{2}$×1×t-$\frac{1}{2}$×1×$\frac{1-t}{1+t}$,
=1-$\frac{1}{2}$t-$\frac{1}{2}$•$\frac{1-t}{1+t}$=1-$\frac{1}{2}$t-$\frac{1}{2}$(-1+$\frac{2}{1+t}$),
=1+$\frac{1}{2}$-$\frac{t}{2}$-$\frac{1}{t+1}$,
=2-($\frac{t+1}{2}$+$\frac{1}{t+1}$),
由于1+t>0,
则S=2-($\frac{t+1}{2}$+$\frac{1}{t+1}$)≤2-2$\sqrt{\frac{t+1}{2}•\frac{1}{t+1}}$=2-$\sqrt{2}$,当且仅当$\frac{t+1}{2}$=$\frac{1}{t+1}$,即t=$\sqrt{2}$-1时等号成立,
故探照灯照射在正方形ABCD内部区域的面积S最多为2-$\sqrt{2}$平方百米.
点评 本题考查三角函数知识的运用,考查和角公式的运用,考查面积的最值,考查学生分析解决问题的能力,属于中档题.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com