练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】某建筑公司打算在一处工地修建一座简易储物间.该储物间室内地面呈矩形形状，面积为，并且一面紧靠工地现有围墙，另三面用高度一定的矩形彩钢板围成，顶部用防雨布遮盖，其平面图如图所示.已知该型号彩钢板价格为100元/米，整理地面及防雨布总费用为500元，不受地形限制，不考虑彩钢板的厚度，记与墙面平行的彩钢板的长度为米.

    （1）用表示修建储物间的总造价（单位：元）；

    （2）如何设计该储物间，可使总造价最低？最低总造价为多少元？

    【答案】（1）（2）与墙面平行的彩钢板长度为10米，另两边长度为5米，可使储物间总造价最低，最低总造价为2500元

    【解析】

    （1）首先求出彩钢板的长度，根据总造价彩钢长度整理地面及防雨布总费用，即可求解.

    （2）利用基本不等式即可求解.

    解：（1）由题意，建造储物间所需彩钢板总长度为米，

    则.

    （2），.

    当且仅当即时等号成立.

    此时，，.

    与墙面平行的彩钢板长度为10米，另两边长度为5米，

    可使储物间总造价最低，最低总造价为2500元.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知圆M的圆心M在x轴上，半径为，直线被圆M截得的弦长为，且圆心M在直线l的上方.

    （1）求圆的方程；

    （2）设，，若圆M是的内切圆，求AC，BC边所在直线的斜率（用t表示）；

    （3）在（2）的条件下求的面积S的最大值及对应的t值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】阅读如图所示的程序框图，解答下列问题：

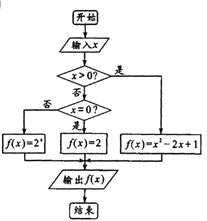
    （1）求输入的的值分别为时，输出的的值；

    （2）根据程序框图，写出函数（）的解析式；并求当关于的方程有三个互不相等的实数解时，实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数．

    （1）若函数是R上的单调增函数，求实数a的取值范围；

    （2）设， 是的导函数．

    ①若对任意的，求证：存在使；

    ②若，求证： ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数 的部分图象如图所示，则函数图象的一个对称中心可能为（ ）

    A. B. C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】(2017·金华调研)如图，AB＝BE＝BC＝2AD＝2，且AB⊥BE，∠DAB＝60°，AD∥BC，BE⊥AD.

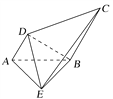
    (1)求证：平面ADE⊥平面BDE；

    (2)求直线AD与平面DCE所成角的正弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）若， 都是从0，1，2，3，4五个数中任取的一个数，求上述函数有零点的概率；

    （2）若， 都是从区间上任取的一个数，求成立的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设椭圆 ()的一个焦点点为椭圆内一点,若椭圆上存在一点，使得，则椭圆的离心率的取值范围是（ ）

    A. B. C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知，，圆上的动点T满足：线段TQ的垂直平分线与线段TP相交于点K．

    Ⅰ求点K的轨迹C的方程；

    Ⅱ经过点的斜率之积为的两条直线，分别与曲线C相交于M，N两点，试判断直线MN是否经过定点若是，则求出定点坐标；若否，则说明理由．

    查看答案和解析>>

    同步练习册答案