
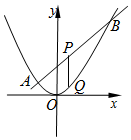
 已知抛物线C:x2=2py(p>0)的焦点为F,直线2x-y+2=0交抛物线C于A,B两点,P是线段AB的中点,过P作x轴的垂线交抛物线C于点Q.
已知抛物线C:x2=2py(p>0)的焦点为F,直线2x-y+2=0交抛物线C于A,B两点,P是线段AB的中点,过P作x轴的垂线交抛物线C于点Q.分析 (1)根据题意,求出直线2x-y+2=0与y轴的交点坐标,即可得抛物线焦点坐标,进而可得抛物线的方程;
(2)联立直线与抛物线的方程,可得x2-4px-4p=0,设A(x1,y1),B(x2,y2),将QA⊥QB转化为$\overrightarrow{QA}•\overrightarrow{QB}=0$,由根与系数的关系分析可得$5{x_1}{x_2}+(4-6p)({x_1}+{x_2})+8{p^2}-8p+4=0$,代入得4p2+3p-1=0,解可得答案.
解答  解:(1)根据题意,直线2x-y+2=0与y轴的交点为(0,2),
解:(1)根据题意,直线2x-y+2=0与y轴的交点为(0,2),
则F(0,2),
∴抛物线C的方程为x2=8y;
(2)由 $\left\{\begin{array}{l}y=2x+2\\{x^2}=2py\end{array}\right.$得:x2-4px-4p=0,
设A(x1,y1),B(x2,y2),则x1+x2=4p,x1x2=-4p,
∴Q(2p,2p),∵QA⊥QB,则$\overrightarrow{QA}•\overrightarrow{QB}=0$,
(x1-2p)(x2-2p)+(y1-2p)(y2-2p)=0,
(x1-2p)(x2-2p)+(2x1+2-2p)(2x2+2-2p)=0,
$5{x_1}{x_2}+(4-6p)({x_1}+{x_2})+8{p^2}-8p+4=0$,
代入得4p2+3p-1=0,解得$p=\frac{1}{4}$或p=-1(舍去)
∴$p=\frac{1}{4}$.
点评 本题考查直线与抛物线的位置关系,关键是由抛物线焦点坐标求出抛物线的方程.


 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案科目:高中数学 来源: 题型:解答题
 如图所示,已知P是?ABCD所在平面外一点,M,N分别是AB,PC的中点,平面PAD∩平面PBC=l.
如图所示,已知P是?ABCD所在平面外一点,M,N分别是AB,PC的中点,平面PAD∩平面PBC=l.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
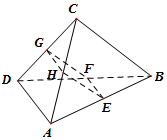 (理科)如图,在空间四面体ABCD中,若E,F,G,H分别是AB,BD,CD,AC的中点,且AD⊥BC
(理科)如图,在空间四面体ABCD中,若E,F,G,H分别是AB,BD,CD,AC的中点,且AD⊥BC查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 28π | B. | $\frac{{28\sqrt{7}π}}{3}$ | C. | 32π | D. | $\frac{{64\sqrt{2}π}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向右平移$\frac{π}{4}$个单位,再向上平移1个单位 | |
| B. | 向左平移$\frac{π}{4}$个单位,再向下平移1个单位 | |
| C. | 向右平移$\frac{π}{2}$个单位,再向上平移1个单位 | |
| D. | 向左平移$\frac{π}{2}$个单位,再向下平移1个单位 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | α<β | B. | α>β | ||
| C. | α=β | D. | 无法确定α与β大小 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com