
【题目】惠州市某学校高三年级模拟考试的数学试题是全国I卷的题型结构,其中第22、23题为选做题,考生只需从中任选一题作答.已知文科数学和理科数学的选做题题目无任何差异,该校参加模拟考试学生共1050人,其中文科学生150人,理科学生900人.在测试结束后,数学老师对该学校全体高三学生选做的22题和23题得分情况进行了统计,22题统计结果如下表1,23题统计结果如下表2.
表1
22题得分 | 0 | 3 | 5 | 8 | 10 |
理科人数 | 50 | 70 | 80 | 100 | 500 |
文科人数 | 5 | 20 | 10 | 5 | 70 |
表2
23题得分 | 0 | 3 | 5 | 8 | 10 |
理科人数 | 10 | 10 | 15 | 25 | 40 |
文科人数 | 5 | 5 | 25 | 0 | 5 |
(1)在答卷中完成如下![]() 列联表,并判断能否至少有
列联表,并判断能否至少有![]() 的把握认为“选做22题或23题”与“学生的科类(文理)”有关系;
的把握认为“选做22题或23题”与“学生的科类(文理)”有关系;
选做22题 | 选做23题 | 合计 | |
文科人数 | 110 | ||
理科人数 | 100 | ||
总计 | 1050 |
(2)在第23题得分为0的学生中,按分层抽样的方法随机抽取6人进行答疑辅导,并在辅导后从这6人中随机抽取2人进行测试,求被抽中进行测试的2名学生均为理科生的概率.
参考公式: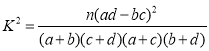 ,其中
,其中![]() .
.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
【答案】(1)列联表见解析,有;(2)![]() .
.
【解析】
(1)根据题意填写![]() 列联表,计算观测值,对照临界值得出结论;
列联表,计算观测值,对照临界值得出结论;
(2)由分层抽样法求得被选取的6名学生中理科生和文科生人数,进而写出从6名学生中随机抽取2名的所有基本事件以及被抽中的2名学生均为理科生的基本事件,进而求出相应的概率.
解:(1)根据题意填写![]() 列联表如下,
列联表如下,
选做22题 | 选做23题 | 合计 | |
文科人数 | 110 | 40 | 150 |
理科人数 | 800 | 100 | 900 |
总计 | 910 | 140 | 1050 |
由表中数据,计算![]()
![]()
![]()
所以有![]() 的把握认为“选做题的选择”与“文、理科的科类”有关;
的把握认为“选做题的选择”与“文、理科的科类”有关;
(2)由分层抽样的方法可知在被选取的6名学生中理科生有4名,文科生有2名,
记4名理科生为![]() ,2名文科生为
,2名文科生为![]() ,
,
从这6名学生中随机抽取2名,全部可能的基本事件共15种
分别是:![]()
![]()
![]()
被抽中的2名学生均为理科生的基本事件是:![]() ,有6种,
,有6种,
故所求的概率为![]()
所以被抽中进行测试的2名学生均为理科生的概率为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知6名某疾病病毒密切接触者中有1名感染病毒,其余5名健康,需要通过化验血液来确定感染者.血液化验结果呈阳性的即为感染者,呈阴性即为健康.
(1)若从这6名密切接触者中随机抽取3名,求抽到感染者的概率;
(2)血液化验确定感染者的方法有:①逐一化验;②分组混合化验:先将血液分成若干组,对组内血液混合化验,若化验结果呈阴性,则该组血液不含病毒;若化验结果呈阳性,则对该组的备份血液逐一化验,直至确定感染者.
(i)采取逐一化验,求所需检验次数![]() 的数学期望;
的数学期望;
(ii)采取平均分组混合化验(每组血液份数相同),依据所需化验总次数的期望,选择合理的平均分组方案.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 的内角A,B,C所对的边分别是a,b,c,其面积S
的内角A,B,C所对的边分别是a,b,c,其面积S![]() .
.
(1)若a![]() ,b
,b![]() ,求cosB.
,求cosB.
(2)求sin(A+B)+sinBcosB+cos(B﹣A)的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为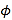 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程和
的普通方程和![]() 的直角坐标方程;
的直角坐标方程;
(2)已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,点
,点![]() 是曲线
是曲线![]() 与
与![]() 的交点,点
的交点,点![]() 是曲线
是曲线![]() 与
与![]() 的交点,
的交点,![]() 、
、![]() 均异于原点
均异于原点![]() ,且
,且![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且满足
,且满足![]() ,
,![]() ,设
,设![]() ,
,![]() .
.
(Ⅰ)求证:数列![]() 是等比数列;
是等比数列;
(Ⅱ)若![]() ,
,![]() ,求实数
,求实数![]() 的最小值;
的最小值;
(Ⅲ)当![]() 时,给出一个新数列
时,给出一个新数列![]() ,其中
,其中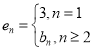 ,设这个新数列的前
,设这个新数列的前![]() 项和为
项和为![]() ,若
,若![]() 可以写成
可以写成![]() (
(![]() ,
,![]() 且
且![]() ,
,![]() )的形式,则称
)的形式,则称![]() 为“指数型和”.问
为“指数型和”.问![]() 中的项是否存在“指数型和”,若存在,求出所有“指数型和”;若不存在,请说明理由.
中的项是否存在“指数型和”,若存在,求出所有“指数型和”;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com