Question

【题目】已知抛物线，点与抛物线的焦点关于原点对称，动点到点的距离与到点的距离之和为4.

（1）求动点的轨迹；

（2）若，设过点的直线与的轨迹相交于两点，当的面积最大时，求直线的方程.

Answer 1

【答案】（1）详见解析（2）或

【解析】

（1）先求的坐标，若，则动点的轨迹不存在；若，则动点的轨迹为线段；若，则动点的轨迹为椭圆.

（2）直线的斜率必存在，可先联立直线方程和椭圆的方程，消元后利用韦达定理可求的长，再求出到直线的距离后可得面积表达式，最后利用基本不等式可得面积何时最大并能求出此时直线的方程.

（1）①当时，的轨迹不存在.

②当时，的轨迹为一线段，方程为；

③当时，的轨迹为焦点在轴上的椭圆，方程为.

（2）若，则的轨迹方程为 .

当轴时不合题意， 故设，，.

将代入得.

由得，，

解得或.

由韦达定理得， ，

.

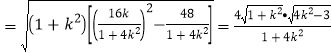又点到直线的距离，

，其中或.

令，则且，

当且仅当即,时等号成立,

所以，当的面积最大时，的方程为或.

方法二：若，则的轨迹方程为.

当轴时不合题意， 故设，，，且.

将代入得.

由得，，

解得或.

由韦达定理得，，

，，

令，则且，

当且仅当即,时等号成立,

所以，当的面积最大时，的方程为或.