
【题目】已知△ABC的三个顶点是A(4,0),B(6,7),C(0,3).
(1)求过点A与BC平行的直线方程.
(2)求过点B,并且在两个坐标轴上截距相等的直线方程.
【答案】
(1)解:根据题意,B(6,7),C(0,3),则KBC= ![]() =
= ![]() ,
,
设要求直线的方程y= ![]() x+b,
x+b,
又由直线过点A(4,0),
则有0= ![]() ×4+b,解可得b=﹣
×4+b,解可得b=﹣ ![]() ,
,
则要求直线的方程为:y= ![]() x﹣
x﹣ ![]() ;
;
(2)解:B(6,7),
若要求的直线过原点,则其方程为y= ![]() x,
x,
若要求的直线不过原点,设其方程为: ![]() +
+ ![]() =1,即x+y=a,
=1,即x+y=a,
要求直线过点B,则有6+7=a=13,
此时直线的方程为x+y=13;
过点B,并且在两个坐标轴上截距相等的直线方程为y= ![]() x和x+y=13.
x和x+y=13.
【解析】(1)根据题意,计算可得直线BC的斜率,可以设要求直线的方程y= ![]() x+b,将点A的坐标代入直线方程可得b的值,解可得要求直线的方程;(2)根据题意,分2种情况讨论:若要求的直线过原点,由点B的坐标易得直线的方程;若要求的直线不过原点,设其方程为:
x+b,将点A的坐标代入直线方程可得b的值,解可得要求直线的方程;(2)根据题意,分2种情况讨论:若要求的直线过原点,由点B的坐标易得直线的方程;若要求的直线不过原点,设其方程为: ![]() +
+ ![]() =1,将点B的坐标代入直线方程可得a的值,解可得要求直线的方程.
=1,将点B的坐标代入直线方程可得a的值,解可得要求直线的方程.


科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C的对边分别是a,b,c,若(2a﹣c)cosB=bcosC.
(1)求角B的大小,
(2)若a=3,△ABC的面积为 ![]() ,求
,求 ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在雅安发生地震灾害之后,救灾指挥部决定建造一批简易房,供灾区群众临时居住,房形为长方体,高2.5米,前后墙用2.5米高的彩色钢板,两侧用2.5米高的复合钢板,两种钢板的价格都用长度来计算(即钢板的高均为2.5米,用长度乘以单价就是这块钢板的价格),每米单价:彩色钢板为450元,复合钢板为200元,房顶用其他材料建造,每平方米材料费为200元,每套房材料费控制在32000元以内.
(1)设房前面墙的长为x,两侧墙的长为y,一套简易房所用材料费为p,试用x,y表示p;
(2)一套简易房面积S的最大值是多少?当S最大时,前面墙的长度是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,四棱锥P﹣ABCD中平面PAB⊥平面ABCD,底面ABCD是正方形.点M是棱PC的中点 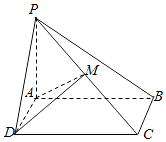
(1)记平面ADM与平面PBC的交线是l,试判断直线l与BC的位置关系,并加以证明.
(2)若 ![]() ,求证PB⊥平面ADM,并求直线PC与平面ADM所成角的正弦值.
,求证PB⊥平面ADM,并求直线PC与平面ADM所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设l,m是两条不同的直线,α是一个平面,则下列命题正确的是( )
A.若l⊥m,mα,则l⊥α
B.若l⊥α,l∥m,则m⊥α
C.若l∥α,mα,则l∥m
D.若l∥α,m∥α,则l∥m
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线f(x)= ![]() (x>0)上有一点列Pn(xn , yn)(n∈N*),过点Pn在x轴上的射影是Qn(xn , 0),且x1+x2+x3+…+xn=2n+1﹣n﹣2.(n∈N*)
(x>0)上有一点列Pn(xn , yn)(n∈N*),过点Pn在x轴上的射影是Qn(xn , 0),且x1+x2+x3+…+xn=2n+1﹣n﹣2.(n∈N*)
(1)求数列{xn}的通项公式;
(2)设四边形PnQnQn+1Pn+1的面积是Sn , 求Sn;
(3)在(2)条件下,求证: ![]() +
+ ![]() +…+
+…+ ![]() <4.
<4.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某产品的三个质量指标分别为x,y,z,用综合指标S=x+y+z评价该产品的等级.若S≤4,则该产品为一等品.现从一批该产品中,随机抽取10件产品作为样本,其质量指标列表如下:
产品编号 | A1 | A2 | A3 | A4 | A5 |
质量指标 | (1,1,2) | (2,1,1) | (2,2,2) | (1,1,1) | (1,2,1) |
产品编号 | A6 | A7 | A8 | A9 | A10 |
质量指标 | (1,2,2) | (2,1,1) | (2,2,1) | (1,1,1) | (2,1,2) |
(1)利用上表提供的样本数据估计该批产品的一等品率.
(2)在该样品的一等品中,随机抽取2件产品, ①用产品编号列出所有可能的结果;
②设事件B为“在取出的2件产品中,每件产品的综合指标S都等于4”,求事件B发生的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com