
 x3+ax2+bx����f�䣨-1��=0��
x3+ax2+bx����f�䣨-1��=0���⣺��1�������⣬��
��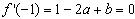 ��
��
�Ӷ�
��
�� ��
�� ��
��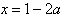
�ٵ�a>1ʱ��
��x�仯ʱ�� ��
�� �ı仯������±���
�ı仯������±��� 
�ɴ˵ã�����f��x���ĵ���������Ϊ ��
�� ������������Ϊ
������������Ϊ ��
��
�ڵ� ʱ��
ʱ��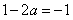 ����ʱ��
����ʱ�� ��������ҽ���
��������ҽ��� ����
����
�ʺ���f��x���ĵ���������ΪR��
�۵� ʱ��
ʱ��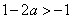 ��ͬ���ɵã�����f��x���ĵ���������Ϊ
��ͬ���ɵã�����f��x���ĵ���������Ϊ ��
�� ��
��
����������Ϊ
���ϣ��� ʱ������f��x���ĵ���������Ϊ
ʱ������f��x���ĵ���������Ϊ ��
��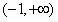 ������������Ϊ
������������Ϊ ��
��
�� ʱ������f��x���ĵ���������ΪR��
ʱ������f��x���ĵ���������ΪR��
�� ʱ������f��x���ĵ���������Ϊ
ʱ������f��x���ĵ���������Ϊ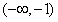 ��
�� ������������Ϊ
������������Ϊ ��
��
��2����i���� ��
��
�� ��
��
�ɣ�1����f��x��������Ϊ ��
��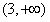 ������������Ϊ
������������Ϊ ��
��
���Ժ���f��x���� ��ȡ�ü�ֵ��
��ȡ�ü�ֵ��
��M�� ����N��
����N�� ����
����
�۲��ͼ������������
�ٵ�m��-1������-1���仯��3ʱ���߶�MP��б��������f��x���ڵ�P�����ߵ�б��֮��Kmp- ��ֵ����������Ϊ����
��ֵ����������Ϊ����
���߶�MP�������Ƿ�������H��P�Ĺ�������Kmp- ��m�����������еĹ�����
��m�����������еĹ�����
��Kmp- =0��Ӧ��λ�ÿ������ٽ�㣬���Ʋ⣺����Kmp-
=0��Ӧ��λ�ÿ������ٽ�㣬���Ʋ⣺����Kmp- ��m���������t��Сֵ��
��m���������t��Сֵ��
�������֤����ȷ����t��Сֵ
����f��x���ڵ� ��������б��
���������
��MP���Kmp
��Kmp- =0ʱ�����
=0ʱ�����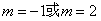
ֱ��MP�ķ���Ϊ
��
�� ʱ��
ʱ�� ��
�� ��ֻ��һ�����
��ֻ��һ����� ��
��
���жϺ���f��x���� �ϵ�����������
�ϵ����������� �ϵ����ݼ���
�ϵ����ݼ���
�� ��
��
����g��x���� ��û����㣬
��û����㣬
���߶�MP������f��x��û������M��P�Ĺ����㡣
�� ʱ��
ʱ��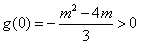 ��
��
���Դ��� ʹ��
ʹ��
���� ʱ��MP������f��x��������M��P�Ĺ�����
ʱ��MP������f��x��������M��P�Ĺ�����
���ϣ�t����СֵΪ2��
��ii�����ƣ�i�����еĹ۲죬�ɵ�m��ȡֵ��ΧΪ ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��֪����f��x��=Asin����x+�գ���x��R��A��0���أ�0��|��|��
��֪����f��x��=Asin����x+�գ���x��R��A��0���أ�0��|��|��| �� |
| 2 |
A��f(x)=2sin(��x+
| ||
B��f(x)=2sin(2��x+
| ||
C��f(x)=2sin(��x+
| ||
D��f(x)=2sin(2��x+
|
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| 1 |
| 3 |
| f��(x) |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| x |
| a |
| b |
| x |
| 4c2 |
| k(k+c) |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���Ϻ�ģ�� ���ͣ������
| x |
| a |
| b |
| x |
| 4c2 |
| k(k+c) |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������һģ ���ͣ������
| 1 |
| 3 |
| f��(x) |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com