
【题目】如图,在各棱长均为![]() 的三棱柱
的三棱柱![]() 中,侧面
中,侧面![]() 底面
底面![]() ,
, ![]() .
.
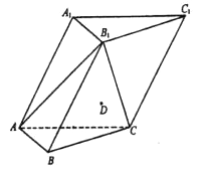
(1)求侧棱![]() 与平面
与平面![]() 所成角的正弦值的大小;
所成角的正弦值的大小;
(2)已知点![]() 满足
满足![]() ,在直线
,在直线![]() 上是否存在点
上是否存在点![]() ,使
,使![]() 平面
平面![]() ?若存在,请确定点
?若存在,请确定点![]() 的位置,若不存在,请说明理由.
的位置,若不存在,请说明理由.
【答案】(1)![]() (2)恰好为
(2)恰好为![]() 点.
点.
【解析】【试题分析】(1)作![]() 于点
于点![]() ,得
,得![]() 平面
平面![]() .由此以
.由此以![]() 为坐标原点建立空间直角坐标系,通过计算直线
为坐标原点建立空间直角坐标系,通过计算直线![]() 的方向向量和平面
的方向向量和平面![]() 的法向量,来求得直线与平面所称角的正弦值.(2)假设存在点
的法向量,来求得直线与平面所称角的正弦值.(2)假设存在点![]() 符合题意,设点
符合题意,设点![]() 的坐标为
的坐标为![]() .结合直线
.结合直线![]() 的方向向量和平面
的方向向量和平面![]() 的法向量垂直,且
的法向量垂直,且![]() ,可求得
,可求得![]() 点的坐标.
点的坐标.
【试题解析】
解:(1)∵侧面![]() 底面
底面![]() ,作
,作![]() 于点
于点![]() ,
,
∴![]() 平面
平面![]() .
.
又![]() ,且各棱长都相等,
,且各棱长都相等,
∴![]() ,
, ![]() ,
, ![]() .
.
故以![]() 为坐标原点,建立如图所示的空间直角坐标系
为坐标原点,建立如图所示的空间直角坐标系![]() ,则,
,则,
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
∴![]() ,
, ![]() ,
, ![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,
,
则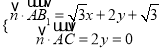 ,解得
,解得![]() .由
.由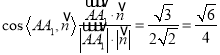 .
.
而侧棱![]() 与平面
与平面![]() 所成角,即是向量
所成角,即是向量![]() 与平面
与平面![]() 的法向量所成锐角的余角,
的法向量所成锐角的余角,
∴侧棱![]() 与平面
与平面![]() 所成角的正弦值的大小为
所成角的正弦值的大小为![]() .
.
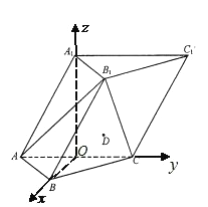
(2)∵![]() ,而
,而![]() ,
, ![]() ,
,
∴![]() ,又∵
,又∵![]() ,∴点
,∴点![]() 的坐标为
的坐标为![]() .
.
假设存在点![]() 符合题意,则点
符合题意,则点![]() 的坐标可设为
的坐标可设为![]() ,∴
,∴![]() .
.
∵![]() 平面
平面![]() ,
, ![]() 为平面
为平面![]() 的法向量,
的法向量,
∴由![]() ,得
,得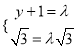 ,∴
,∴![]() .
.
又![]() 平面
平面![]() ,故存在点
,故存在点![]() ,使
,使![]() 平面
平面![]() ,其坐标为
,其坐标为![]() ,
,
即恰好为![]() 点.
点.


 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案科目:高中数学 来源: 题型:
【题目】某翻译处有8名翻译,其中有小张等3名英语翻译,小李等3名日语翻译,另外2名既能翻译英语又能翻译日语,现需选取5名翻译参加翻译工作,3名翻译英语,2名翻译日语,且小张与小李恰有1人选中,则有____种不同选取方法.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD是正方形,PA![]() 平面ABCD,EB//PA,AB=PA=4,EB=2,F为PD的中点.
平面ABCD,EB//PA,AB=PA=4,EB=2,F为PD的中点.
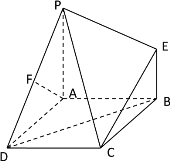
(1)求证AF![]() PC
PC
(2)BD//平面PEC
(3)求二面角D-PC-E的大小
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】通过随机询问110名性别不同的大学生是否爱好某项运动,得到如下的列联表:
男 | 女 | 总计 | |
爱好 | 40 | 20 | 60 |
不爱好 | 20 | 30 | 50 |
总计 | 60 | 50 | 110 |
由![]() 算得,
算得,![]()
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
参照附表,得到的正确结论是 ( )
A. 在犯错误的概率不超过1%的前提下,认为“爱好该项运动与性别有关”
B. 在犯错误的概率不超过1%的前提下,认为“爱好该项运动与性别无关”
C. 有99.9%以上的把握认为“爱好该项运动与性别有关”
D. 有99.9%以上的把握认为“爱好该项运动与性别无关”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下图是某省从1月21日至2月24日的新冠肺炎每日新增确诊病例变化曲线图.

若该省从1月21日至2月24日的新冠肺炎每日新增确诊人数按日期顺序排列构成数列![]() ,
,![]() 的前n项和为
的前n项和为![]() ,则下列说法中正确的是( )
,则下列说法中正确的是( )
A.数列![]() 是递增数列B.数列
是递增数列B.数列![]() 是递增数列
是递增数列
C.数列![]() 的最大项是
的最大项是![]() D.数列
D.数列![]() 的最大项是
的最大项是![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱椎![]() 中,
中, ![]() 是棱
是棱![]() 上一点,且
上一点,且![]() ,底面
,底面![]() 是边长为2的正方形,
是边长为2的正方形, ![]() 为正三角形,且平面
为正三角形,且平面![]() 平面
平面![]() ,平面
,平面![]() 与棱
与棱![]() 交于点
交于点![]() .
.
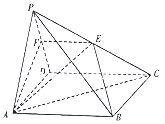
(1)求证:平面![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设中心在原点,焦点在![]() 轴上的椭圆
轴上的椭圆![]() 过点
过点![]() ,且离心率为
,且离心率为![]() .
.![]() 为
为![]() 的右焦点,
的右焦点,![]() 为
为![]() 上一点,
上一点,![]() 轴,
轴,![]() 的半径为
的半径为![]() .
.
(1)求![]() 和
和![]() 的方程;
的方程;
(2)若直线![]() 与
与![]() 交于
交于![]() 两点,与
两点,与![]() 交于
交于![]() 两点,其中
两点,其中![]() 在第一象限,是否存在
在第一象限,是否存在![]() 使
使![]() ?若存在,求
?若存在,求![]() 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com