
【题目】【选做题】本题包括A、B、C、D四小题,请选定其中两小题,并在相应的答题区域内作答.若多做,则按作答的前两小题评分.解答时应写出文字说明、证明过程或演算步骤.
(1)A.【选修4—1几何证明选讲】
如图,在△ABC中,∠ABC=90°,BD⊥AC , D为垂足,E是BC的中点,求证:∠EDC=∠ABD.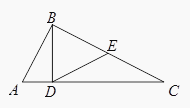
(2)B.【选修4—2:矩阵与变换】
已知矩阵A= ![]() 矩阵B的逆矩阵B﹣1=
矩阵B的逆矩阵B﹣1= 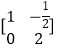 ,求矩阵AB.
,求矩阵AB.
(3)【选修4—4:坐标系与参数方程】在平面直角坐标系xOy中,已知直线l的参数方程为 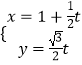 (t为参数),椭圆C的参数方程为
(t为参数),椭圆C的参数方程为 ![]() (
( ![]() 为参数).设直线l与椭圆C相交于A , B两点,求线段AB的长.
为参数).设直线l与椭圆C相交于A , B两点,求线段AB的长.
(4)D. 设a>0,|x﹣1|< ![]() ,|y﹣2|<
,|y﹣2|< ![]() ,求证:|2x+y﹣4|<a.
,求证:|2x+y﹣4|<a.
【答案】
(1)
解:由 ![]() 可得
可得 ![]() ,
,
由 ![]() 是
是 ![]() 中点可得
中点可得 ![]() ,
,
则 ![]() ,
,
由 ![]() 可得
可得 ![]() ,
,
由 ![]() 可得
可得 ![]() ,
,
因此 ![]() ,
,
又 ![]() 可得
可得 ![]()
(2)
解:  ,因此
,因此 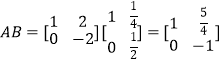 .
.
(3)
解:直线 ![]() 方程化为普通方程为
方程化为普通方程为 ![]() ,
,
椭圆 ![]() 方程化为普通方程为
方程化为普通方程为 ![]() ,
,
联立得 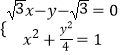 ,解得
,解得 ![]() 或
或 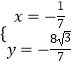 ,
,
因此 ![]()
(4)
证明:由 ![]() 可得
可得 ![]() ,
,
![]()
【解析】A、依题意,知∠BDC=90°,∠EDC=∠C,利用∠C+∠DBC=∠ABD+∠DBC=90°,可得∠ABD=∠C,从而可证得结论.
B、依题意,利用矩阵变换求得B=(B﹣1)﹣1= ![]() =
= ![]() ,再利用矩阵乘法的性质可求得答案.
,再利用矩阵乘法的性质可求得答案.
C、分别化直线与椭圆的参数方程为普通方程,然后联立方程组,求出直线与椭圆的交点坐标,代入两点间的距离公式求得答案.
D、运用绝对值不等式的性质:|a+b|≤|a|+|b|,结合不等式的基本性质,即可得证.
【考点精析】解答此题的关键在于理解直线的参数方程的相关知识,掌握经过点![]() ,倾斜角为
,倾斜角为![]() 的直线
的直线![]() 的参数方程可表示为
的参数方程可表示为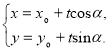 (
(![]() 为参数),以及对椭圆的参数方程的理解,了解椭圆
为参数),以及对椭圆的参数方程的理解,了解椭圆![]()
![]() 的参数方程可表示为
的参数方程可表示为![]() .
.


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:高中数学 来源: 题型:
【题目】袋子中放有大小和形状相同的小球若干,其中标号为0的小球1个,标号为1的小球1个,标号为2的小球2个.从袋子中不放回地随机抽取小球两个,每次抽取一个球,记第一次取出的小球标号为![]() ,第二次取出的小球标号为
,第二次取出的小球标号为![]() .
.
(1)记事件![]() 表示“
表示“![]() ”,求事件
”,求事件![]() 的概率;
的概率;
(2)在区间![]() 内任取两个实数
内任取两个实数![]() ,
,![]() ,求“事件
,求“事件![]() 恒成立”的概率.
恒成立”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂利用辐射对食品进行灭菌消毒,现准备在该厂附近建一职工宿舍,并对宿舍进行防辐射处理,建房防辐射材料的选用与宿舍到工厂距离有关.若建造宿舍的所有费用![]() (万元)和宿舍与工厂的距离
(万元)和宿舍与工厂的距离![]() 的关系为:
的关系为: ![]() .为了交通方便,工厂与宿舍之间还要修一条简易便道,已知修路每公里成本为
.为了交通方便,工厂与宿舍之间还要修一条简易便道,已知修路每公里成本为![]() 万元,工厂一次性补贴职工交通费
万元,工厂一次性补贴职工交通费![]() 万元.设
万元.设![]() 为建造宿舍、修路费用与给职工的补贴之和.
为建造宿舍、修路费用与给职工的补贴之和.
⑴求![]() 的表达式;
的表达式;
⑵宿舍应建在离工厂多远处,可使总费用![]() 最小,并求最小值.
最小,并求最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知以M为圆心的圆M:x2+y2﹣12x﹣14y+60=0及其上一点A(2,4).
(1)设圆N与x轴相切,与圆M外切,且圆心N在直线x=6上,求圆N的标准方程;
(2)设平行于OA的直线l与圆M相交于B、C两点,且BC=OA,求直线l的方程;
(3)设点T(t,0)满足:存在圆M上的两点P和Q,使得 ![]() ,求实数t的取值范围。
,求实数t的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,M,N,K分别是正方体ABCD—A1B1C1D1的棱AB,CD,C1D1的中点.

求证:(1)AN∥平面A1MK;
(2)平面A1B1C⊥平面A1MK.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,平面![]() 平面
平面![]() ,四边形
,四边形![]() 和
和![]() 是全等的等腰梯形,其中
是全等的等腰梯形,其中![]() ,且
,且![]() ,点
,点![]() 为
为![]() 的中点,点
的中点,点![]() 是
是![]() 的中点.
的中点.

(I)请在图中所给的点中找出两个点,使得这两个点所在直线与平面![]() 垂直,并给出证明;
垂直,并给出证明;
(II)求二面角![]() 的余弦值;
的余弦值;
(III)在线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ?如果存在,求出
?如果存在,求出![]() 的长度,如果不存在,请说明理由.
的长度,如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}满足a3=2,前3项和为S3=![]() .
.
(1)求{an}的通项公式;
(2)设等比数列{bn}满足b1=a1,b4=a15,求{bn}的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() (其中
(其中![]() ,
,![]() ,
,![]() )的图象的两条相邻对称轴之间的距离为
)的图象的两条相邻对称轴之间的距离为![]() ,且图象上一个最低点为
,且图象上一个最低点为![]() .
.
(1)求函数![]() 的解析式;
的解析式;
(2)当![]() 时,求函数
时,求函数![]() 的值域;
的值域;
(3)若方程![]() 在
在![]() 上有两个不相等的实数根
上有两个不相等的实数根![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,设抛物线y2=2px(p>0)的焦点为F,抛物线上的点A到y轴的距离等于|AF|﹣1,
(1)求p的值;
(2)若直线AF交抛物线于另一点B,过B与x轴平行的直线和过F与AB垂直的直线交于点N,AN与x轴交于点M,求M的横坐标的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com