
【题目】已知直线![]() ,
,![]() ,过点
,过点![]() 的直线
的直线![]() 分别与直线
分别与直线![]() ,
,![]() 交于
交于![]() ,其中点
,其中点![]() 在第三象限,点
在第三象限,点![]() 在第二象限,点
在第二象限,点![]() ;
;
(1)若![]() 的面积为
的面积为![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)直线![]() 交于
交于![]() 点
点![]() ,直线
,直线![]() 交
交![]() 于点
于点![]() ,若
,若![]() 直线的斜率均存在,分别设为
直线的斜率均存在,分别设为![]() ,判断
,判断![]() 是否为定值?若为定值,求出该定值;若不为定值,说明理由.
是否为定值?若为定值,求出该定值;若不为定值,说明理由.
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:高中数学 来源: 题型:
【题目】设椭圆![]() :
:![]() (
(![]() ),左、右焦点分别是
),左、右焦点分别是![]() 、
、![]() 且
且![]() ,以
,以![]() 为圆心,3为半径的圆与以
为圆心,3为半径的圆与以![]() 为圆心,1为半径的圆相交于椭圆
为圆心,1为半径的圆相交于椭圆![]() 上的点
上的点![]()
(1)求椭圆![]() 的方程;
的方程;
(2)设椭圆![]() :
:![]() ,
,![]() 为椭圆
为椭圆![]() 上任意一点,过点
上任意一点,过点![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,射线
两点,射线![]() 交椭圆
交椭圆![]() 于点
于点![]()
①求![]() 的值;
的值;
②令![]() ,求
,求![]() 的面积
的面积![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设点![]() 、
、![]() 的坐标分别为
的坐标分别为![]() 和
和![]() ,动点P满足
,动点P满足![]() ,设动点P的轨迹为
,设动点P的轨迹为![]() ,以动点P到点
,以动点P到点![]() 距离的最大值为长轴,以点
距离的最大值为长轴,以点![]() 、
、![]() 为左、右焦点的椭圆为
为左、右焦点的椭圆为![]() ,则曲线
,则曲线![]() 和曲线
和曲线![]() 的交点到
的交点到![]() 轴的距离为_________.
轴的距离为_________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国诗词大会的播出引发了全民读书热,某学校语文老师在班里开展了一次诗词默写比赛,班里40名学生得分数据的茎叶图如右图,若规定得分不低于85分的学生得到“诗词达人”的称号,低于85分且不低于70分的学生得到“诗词能手”的称号,其他学生得到“诗词爱好者”的称号.根据该次比赛的成绩按照称号的不同进行分层抽样抽选10名学生,则抽选的学生中获得“诗词能手”称号的人数为( )

A. 6B. 5C. 4D. 2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题正确的是( )
A. 如果两条平行直线中的一条与一个平面平行,那么另一条也与这个平面平行
B. 若一条直线平行于两个相交平面,则这条直线与这两个平面的交线平行
C. 垂直于同一条直线的两条直线相互垂直
D. 若两条直线与第三条直线所成的角相等,则这两条直线互相平行
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点P在曲线C:![]() 上,曲线C在点P处的切线为
上,曲线C在点P处的切线为![]() ,过点P且与直线
,过点P且与直线![]() 垂直的直线与曲线C的另一交点为Q,O为坐标原点,若OP⊥OQ,则点P的纵坐标为_______.
垂直的直线与曲线C的另一交点为Q,O为坐标原点,若OP⊥OQ,则点P的纵坐标为_______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左顶点为
的左顶点为![]() ,离心率为
,离心率为![]() ,点
,点![]() 在椭圆
在椭圆![]() 上.
上.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,直线
两点,直线![]() ,
,![]() 分别与
分别与![]() 轴交于点
轴交于点![]() ,
,![]() ,求证:在
,求证:在![]() 轴上存在点
轴上存在点![]() ,使得无论非零实数
,使得无论非零实数![]() 怎样变化,总有
怎样变化,总有![]() 为直角,并求出点
为直角,并求出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
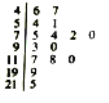
【题目】空气质量指数(Air Quality Index,简称AQI)是定量描述空气质量状况的指数,空气质量按照AQI大小分为六级,0~50为优;51~100为良;101~150为轻度污染;151~200为中度污染;201~300为重度污染;大于300为严重污染.某环保人士从当地某年的AQI记录数据中,随机抽取了15天的AQI数据,用如图所示的茎叶图记录.根据该统计数据,估计此地该年空气质量为优或良的天数约为__________.(该年为366天)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com