
 的特征值及对应的特征向量.
的特征值及对应的特征向量.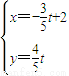 (t为参数).
(t为参数).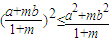 .
.
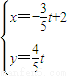 (t为参数).我们易求出曲线C的标准方程及直线l的一般方程,利用直线一圆的位置关系,判断圆心到直线的距离与半径的关系,即可得到答案.
(t为参数).我们易求出曲线C的标准方程及直线l的一般方程,利用直线一圆的位置关系,判断圆心到直线的距离与半径的关系,即可得到答案.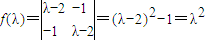 -4λ+3(3分)
-4λ+3(3分)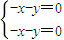 ⇒x+y=0,可取
⇒x+y=0,可取 为属于特征值λ1=1的一个特征向量(8分)
为属于特征值λ1=1的一个特征向量(8分)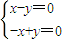 ⇒x-y=0,所以可取
⇒x-y=0,所以可取 为属于特征值λ2=3的一个特征向量.
为属于特征值λ2=3的一个特征向量. 有两个特征值λ1=1,λ2=3;属于λ1=1的一个特征向量为
有两个特征值λ1=1,λ2=3;属于λ1=1的一个特征向量为 ,
, (10分)
(10分) (x-2)(6分)
(x-2)(6分)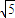 (8分)
(8分)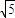 +1(10分)
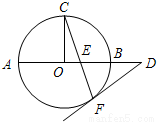
+1(10分)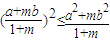 ,即证(a+mb)2≤(1+m)(a2+mb2),
,即证(a+mb)2≤(1+m)(a2+mb2),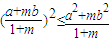 (10分)
(10分)

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
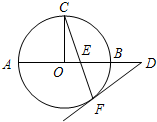 A(选修4-1:几何证明选讲)
A(选修4-1:几何证明选讲)
|
|
| a+mb |
| 1+m |
| a2+mb2 |
| 1+m |
查看答案和解析>>
科目:高中数学 来源: 题型:
 选做题:在A、B、C、D四小题中只能选做2题,每小题10分,共20分.解答应写出文字说明、证明过程或演算步骤.
选做题:在A、B、C、D四小题中只能选做2题,每小题10分,共20分.解答应写出文字说明、证明过程或演算步骤.
|
|
| 2 |
| π |
| 4 |
|
查看答案和解析>>
科目:高中数学 来源: 题型:
 A)选修4-1:几何证明选讲
A)选修4-1:几何证明选讲| 13 |
| 13 |
|
查看答案和解析>>
科目:高中数学 来源: 题型:
 选做题在A、B、C、D四小题中只能选做2题,每小题10分,共计20分.
选做题在A、B、C、D四小题中只能选做2题,每小题10分,共计20分.
|
|
|
| 1 |
| b |
| 1 |
| 2a |
查看答案和解析>>
科目:高中数学 来源: 题型:
 从A,B,C,D四个中选做2个A.选修4-1(几何证明选讲)
从A,B,C,D四个中选做2个A.选修4-1(几何证明选讲)
|
|
| 1 |
| x2-2xy+y2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com