已知菱形
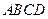
中,
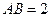
,
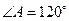
,沿对角线
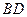
将
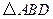
折起,使二面角
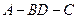
为
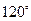
,则点
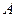
到
所在平面的距离等于
。
先设
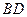
中点为
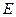
,连接
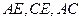
,然后解得
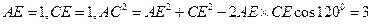
,过点
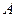
做
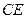
的垂线,即为所求。
练习册系列答案
相关习题
科目:高中数学
来源:不详
题型:解答题
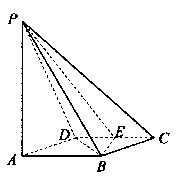
如图所示,四棱锥
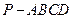
的底面
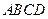
是边长为1的菱形,
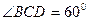
,
E是CD的中点,PA
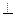
底面ABCD,
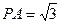
。
(I)证明:平面PBE
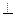
平面PAB;
(II)求二面角A—BE—P和的大小。
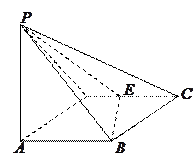
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
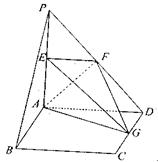
(本小题满分12分)
如图所示,平面
PAD⊥平面
ABCD,
ABCD为正方形,
PA⊥
AD,且
PA=
AD=2,
E,
F,
G分别是线段
PA,
PD,
CD的中点。
(1)求证:
BC//平面
EFG;
(2)求三棱锥
E—
AFG的体积。
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
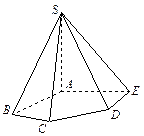
如图,在五棱锥
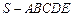
中,
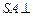
底面
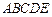
,
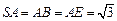
,
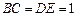
,
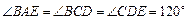
。
(1)证明:
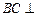
平面
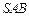
;
(2)求二面角
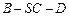
的余弦值。
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
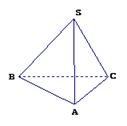
在三棱锥
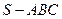
中,
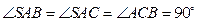
,
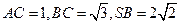
.
(1) 求三棱锥
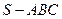
的体积;
(2) 证明:
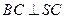
;
(3) 求异面直线SB和AC所成角的余弦值。
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
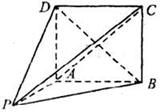
如图,在几何体
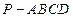
中,面
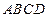
为矩形,
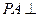
面
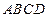
,
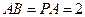
(1)求证;当
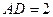
时,平面PBD⊥平面PAC;
(2)当
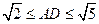
时,求二面角
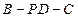
的取值范围。
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
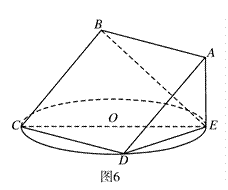
如图6,正方形
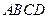
所在平面与圆

所在平面相交于
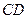
,线段
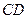
为圆

的弦,
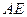
垂直于圆

所在平面,垂足
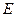
是圆

上异于
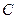
、
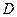
的点,
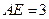
,圆

的直径为9.
(1)求证:平面
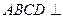
平面
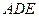
;
(2)求二面角
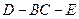
的平面角的正切值.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
如图,在四棱锥
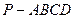
中,底面
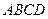
是矩形,已知
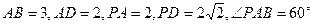
.
(1)证明:
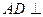
平面
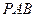
;
(2)求异面直线PC与AD所成的角的大小;
(3)求二面角
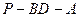
的大小.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
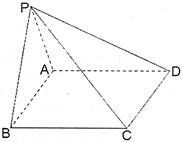
在四棱锥
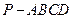
中,
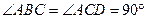
,
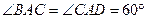
,
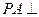
底面
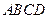
,
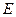
为
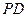
的中点,
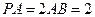
.
(Ⅰ)求四棱锥
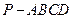
的体积
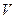
;
(Ⅱ) 求二面角
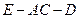
的大小.

查看答案和解析>>

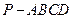 的底面
的底面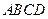 是边长为1的菱形,
是边长为1的菱形,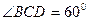 ,
,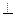 底面ABCD,
底面ABCD,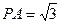 。
。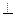 平面PAB;
平面PAB;



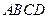 所在平面与圆
所在平面与圆 所在平面相交于
所在平面相交于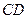 ,线段
,线段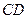 为圆
为圆 的弦,
的弦,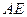 垂直于圆
垂直于圆 所在平面,垂足
所在平面,垂足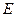 是圆
是圆 上异于
上异于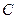 、
、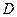 的点,
的点,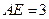 ,圆
,圆 的直径为9.
的直径为9.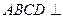 平面
平面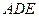 ;
;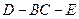 的平面角的正切值.
的平面角的正切值.