
【题目】已知非常数列![]() 满足
满足![]() ,若
,若![]() ,则( )
,则( )
A.存在![]() ,
,![]() ,对任意
,对任意![]() ,
,![]() ,都有
,都有![]() 为等比数列
为等比数列
B.存在![]() ,
,![]() ,对任意
,对任意![]() ,
,![]() ,都有
,都有![]() 为等差数列
为等差数列
C.存在![]() ,
,![]() ,对任意
,对任意![]() ,
,![]() ,都有
,都有![]() 为等差数列
为等差数列
D.存在![]() ,
,![]() ,对任意
,对任意![]() ,
,![]() ,都有
,都有![]() 为等比数列
为等比数列
 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:高中数学 来源: 题型:
【题目】如图,直四棱柱![]() 的底面
的底面![]() 是边长为2的菱形,
是边长为2的菱形,![]() ,
,![]() .
.![]() 、
、![]() 分别为
分别为![]() 和
和![]() 的中点.平面
的中点.平面![]() 与棱
与棱![]() 所在直线交于点
所在直线交于点![]() .
.
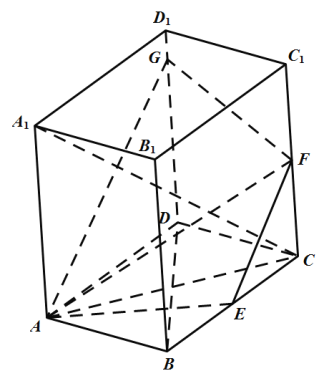
(1)求证:平面![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(3)判断点![]() 是否与点
是否与点![]() 重合.
重合.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,随着![]() 网络的普及和智能手机的更新换代,各种方便的
网络的普及和智能手机的更新换代,各种方便的![]() 相继出世,其功能也是五花八门.某大学为了调查在校大学生使用
相继出世,其功能也是五花八门.某大学为了调查在校大学生使用![]() 的主要用途,随机抽取了
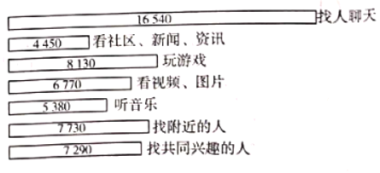
的主要用途,随机抽取了![]() 名大学生进行调查,各主要用途与对应人数的结果统计如图所示,现有如下说法:
名大学生进行调查,各主要用途与对应人数的结果统计如图所示,现有如下说法:
①可以估计使用![]() 主要听音乐的大学生人数多于主要看社区、新闻、资讯的大学生人数;
主要听音乐的大学生人数多于主要看社区、新闻、资讯的大学生人数;
②可以估计不足![]() 的大学生使用
的大学生使用![]() 主要玩游戏;
主要玩游戏;
③可以估计使用![]() 主要找人聊天的大学生超过总数的
主要找人聊天的大学生超过总数的![]() .
.
其中正确的个数为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某软件公司新开发一款学习软件,该软件把学科知识设计为由易到难共12关的闯关游戏.为了激发闯关热情,每闯过一关都奖励若干慧币(一种网络虚拟币).该软件提供了三种奖励方案:第一种,每闯过一关奖励80慧币;第二种,闯过第一关奖励8慧币,以后每一关比前一关多奖励8慧币;第三种,闯过第一关奖励1慧币,以后每一关比前一关奖励翻一番(即增加1倍).游戏规定:闯关者须于闯关前任选一种奖励方案.已知一名闯关者冲关数一定超过3关但不会超过9关,为了得到更多的慧币,他应如何选择奖励方案?
A.选择第一种奖励方案B.选择第二种奖励方案
C.选择第三种奖励方案D.选择的奖励方案与其冲关数有关
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】红铃虫是棉花的主要害虫之一,能对农作物造成严重伤害,每只红铃虫的平均产卵数y和平均温度x有关,现收集了以往某地的7组数据,得到下面的散点图及一些统计量的值.(表中![]() )
)
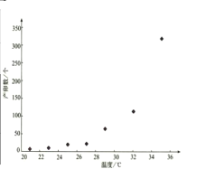
平均温度 | 21 | 23 | 25 | 27 | 29 | 32 | 35 | ||
平均产卵数 | 7 | 11 | 21 | 24 | 66 | 115 | 325 | ||
|
|
|
|
| |||||
27.429 | 81.286 | 3.612 | 40.182 | 147.714 | |||||
(1)根据散点图判断,![]() 与
与![]() (其中
(其中![]() 自然对数的底数)哪一个更适宜作为平均产卵数y关于平均温度x的回归方程类型?(给出判断即可,不必说明理由)并由判断结果及表中数据,求出y关x的回归方程.(计算结果精确到小数点后第三位)
自然对数的底数)哪一个更适宜作为平均产卵数y关于平均温度x的回归方程类型?(给出判断即可,不必说明理由)并由判断结果及表中数据,求出y关x的回归方程.(计算结果精确到小数点后第三位)
(2)根据以往统计,该地每年平均温度达到28℃以上时红铃虫会造成严重伤害,需要人工防治,其他情况均不需要人工防治,记该地每年平均温度达到28℃以上的概率为![]() .
.
①记该地今后5年中,恰好需要3次人工防治的概率为![]() ,求
,求![]() 的最大值,并求出相应的概率p.
的最大值,并求出相应的概率p.
②当![]() 取最大值时,记该地今后5年中,需要人工防治的次数为X,求X的数学期望和方差.
取最大值时,记该地今后5年中,需要人工防治的次数为X,求X的数学期望和方差.
附:线性回归方程系数公式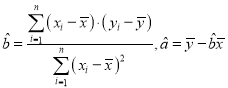 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为缓解日益拥堵的交通状况,不少城市实施车牌竞价策略,以控制车辆数量.某地车牌竞价的原则是:①“盲拍”,即所有参与竞拍的人都是网络报价,每个人并不知晓其他人的报价,也不知道参与当期竞拍的总人数;②竞价时间截止后,系统根据当期车牌配额,按照竞价人的出价从高到低分配名额.某人拟参加2018年10月份的车牌竞价,他为了预测最低成交价,根据竞拍网站的公告,统计了最近5个月参与竞拍的人数(见表):
月份 | 2018.04 | 2018.05 | 2018.06 | 2018.07 | 2018.08 |
月份编号t | 1 | 2 | 3 | 4 | 5 |
竞拍人数y(万人) | 0.5 | 0.6 | m | 1.4 | 1.7 |
(1)由收集数据的散点图发现,可以线性回归模拟竞拍人数y(万人)与月份编号t之间的相关关系.现用最小二乘法求得y关于t的回归方程为![]() ,请求出表中的m的值并预测2018年9月参与竞拍的人数;
,请求出表中的m的值并预测2018年9月参与竞拍的人数;
(2)某市场调研机构对200位拟参加2018年9月车牌竞拍人员的报价价格进行了一个抽样调查,得到如下一个频数表:
报价区间(万元) | [1,2) | [2,3) | [3,4) | [4,5) | [5,6) | [6,7] |
频数 | 20 | 60 | 60 | 30 | 20 | 10 |
(i)求这200位竞拍人员报价的平均值![]() (同一区间的报价可用该价格区间的中点值代替);
(同一区间的报价可用该价格区间的中点值代替);
(ii)假设所有参与竞拍人员的报价X服从正态分布![]() ,且
,且![]() 为(i)中所求的样本平均数
为(i)中所求的样本平均数![]() 的估值,
的估值,![]() .若2018年9月实际发放车牌数量为3174,请你合理预测(需说明理由)竞拍的最低成交价.参考公式及数据:若随机变量Z服从正态分布
.若2018年9月实际发放车牌数量为3174,请你合理预测(需说明理由)竞拍的最低成交价.参考公式及数据:若随机变量Z服从正态分布![]() ,则:
,则:![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现代足球运动是世上开展得最广泛、影响最大的运动项目,有人称它为“世界第一运动”.早在2000多年前的春秋战国时代,就有了一种球类游戏“蹴鞠”,后来经过阿拉伯人传到欧洲,发展成现代足球.1863年10月26日,英国人在伦敦成立了世界上第一个足球运动组织——英国足球协会,并统一了足球规则.人们称这一天是现代足球的诞生日.如图所示,足球表面是由若干黑色正五边形和白色正六边形皮围成的,我们把这些正五边形和正六边形都称为足球的面,任何相邻两个面的公共边叫做足球的棱.已知足球表面中的正六边形的面为20个,则该足球表面中的正五边形的面为______个,该足球表面的棱为______条.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com