
【题目】某宾馆在装修时,为了美观,欲将客房的窗户设计成半径为![]() 的圆形,并用四根木条将圆分成如图所示的9个区域,其中四边形
的圆形,并用四根木条将圆分成如图所示的9个区域,其中四边形![]() 为中心在圆心的矩形,现计划将矩形
为中心在圆心的矩形,现计划将矩形![]() 区域设计为可推拉的窗口.
区域设计为可推拉的窗口.
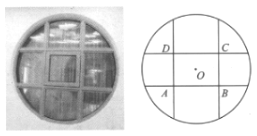
(1)若窗口![]() 为正方形,且面积大于
为正方形,且面积大于![]() (木条宽度忽略不计),求四根木条总长的取值范围;
(木条宽度忽略不计),求四根木条总长的取值范围;
(2)若四根木条总长为![]() ,求窗口
,求窗口![]() 面积的最大值.
面积的最大值.
【答案】(1)![]() (2)
(2)![]()
【解析】
试题(1)长度与面积关系问题,可以考虑利用解不等式求范围,先根据直线与圆位置关系得弦长与圆心到直线距离(即正方形边长一半)关系,再根据面积大于![]() 得一根木条长范围,注意四根木条将圆分成9个区域的隐含条件:
得一根木条长范围,注意四根木条将圆分成9个区域的隐含条件:![]() (2)思路为长度一定,求面积最值,可以考虑利用基本不等式求最值,设
(2)思路为长度一定,求面积最值,可以考虑利用基本不等式求最值,设![]() 所在木条长为
所在木条长为![]() ,
,![]() 所在木条长为
所在木条长为![]() ,则
,则![]() ,而圆中垂径定理得
,而圆中垂径定理得![]() ,因此
,因此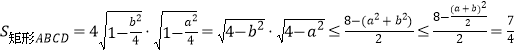
试题解析:解(1)设一根木条长为![]() ,则正方形的边长为
,则正方形的边长为![]()
因为![]() ,所以
,所以![]() ,即
,即![]()
又因为四根木条将圆分成9个区域,所以![]()
所以![]() ;
;
(2)(方法一)设![]() 所在木条长为
所在木条长为![]() ,则
,则![]() 所在木条长为
所在木条长为![]()
因为![]() ,所以
,所以![]()
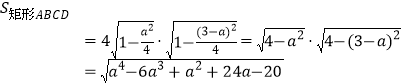
设![]() ,
,![]()
令![]() ,得
,得![]() ,或
,或![]() (舍去),或
(舍去),或![]() (舍去)
(舍去)
列表如下:
|
|
|
|
| + | 0 | - |
|
| 极大值 |
|
所以当![]() 时,
时,![]() ,即
,即![]()
(方法二)设![]() 所在木条长为
所在木条长为![]() ,
,![]() 所在木条长为
所在木条长为![]()
由条件,![]() ,即
,即![]()
因为![]() ,所以
,所以![]() ,从而
,从而![]()
由于![]() ,
,![]()
因为![]()
当且仅当![]() 时,
时,![]()
答:窗口![]() 面积的最大值为
面积的最大值为![]()


科目:高中数学 来源: 题型:
【题目】在倡导低碳、节能减排政策的推动下,越来越多的消费者选择购买新能源汽车.某品牌新能源汽车的行驶里程x(万公里)与该里程内维修保养的总费用y(千元)的统计数据如下:
| 1 | 2 | 3 | 4 | 5 | 6 |
| 0.8 | 1.8 | 3.3 | 4.5 | 4.7 | 6.8 |
(1)根据表中数据建立y关于x的回归方程为![]() .我们认为,若残差绝对值
.我们认为,若残差绝对值![]() ,则该数据为可疑数据,请找出上表中的可疑数据;
,则该数据为可疑数据,请找出上表中的可疑数据;
(2)经过确认,数据采集有误,(1)中可疑数据的维修保养总费用应增加0.7千元.请重新利用线性回归模型拟合数据.(精确到0.01)
附: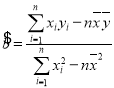 ,
,![]() .
.![]() ,
,![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(13分)设{an}是公比为正数的等比数列a1=2,a3=a2+4.
(Ⅰ)求{an}的通项公式;
(Ⅱ)设{bn}是首项为1,公差为2的等差数列,求数列{an+bn}的前n项和Sn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 中,底面 ABCD为矩形,侧面为正三角形,且平面
中,底面 ABCD为矩形,侧面为正三角形,且平面![]() 平面
平面 ![]() E 为 PD 中点,AD=2.
E 为 PD 中点,AD=2.
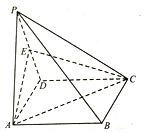
(1)证明平面AEC丄平面PCD;
(2)若二面角![]() 的平面角
的平面角![]() 满足
满足![]() ,求四棱锥
,求四棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知焦距为2![]() 的椭圆
的椭圆![]() :
:![]() 的右顶点为
的右顶点为![]() ,直线
,直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 、
、![]() 两点(
两点(![]() 在
在![]() 的左边),
的左边),![]() 在
在![]() 轴上的射影为
轴上的射影为![]() ,且四边形
,且四边形![]() 是平行四边形.
是平行四边形.
(1)求椭圆![]() 的方程;
的方程;
(2)斜率为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于两个不同的点
交于两个不同的点![]() ,
,![]() .
.
(i)若直线![]() 过原点且与坐标轴不重合,
过原点且与坐标轴不重合,![]() 是直线
是直线![]() 上一点,且
上一点,且![]() 是以
是以![]() 为直角顶点的等腰直角三角形,求
为直角顶点的等腰直角三角形,求![]() 的值;
的值;
(ii)若![]() 是椭圆的左顶点,
是椭圆的左顶点,![]() 是直线
是直线![]() 上一点,且
上一点,且![]() ,点
,点![]() 是
是![]() 轴上异于点
轴上异于点![]() 的点,且以
的点,且以![]() 为直径的圆恒过直线
为直径的圆恒过直线![]() 和
和![]() 的交点,求证:点
的交点,求证:点![]() 是定点.
是定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四个结论:
![]() 两条直线和同一个平面垂直,则这两条直线平行;
两条直线和同一个平面垂直,则这两条直线平行;
![]() 两条直线没有公共点,则这两条直线平行;
两条直线没有公共点,则这两条直线平行;
![]() 两条直线都和第三条直线垂直,则这两条直线平行;
两条直线都和第三条直线垂直,则这两条直线平行;
![]() 一条直线和一个平面内任意直线没有公共点,则这条直线和这个平面平行.
一条直线和一个平面内任意直线没有公共点,则这条直线和这个平面平行.
其中正确的个数为( )
A.0B.1C.2D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P—ABCD中,PA⊥平面ABCD,四边形ABCD为正方形,AB=4,PA=3,点A在PD上的射影为点G,点E在AB上,平面PEC⊥平面PDC.
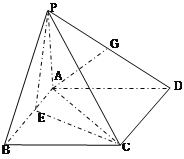
(1)求证:AG∥平面PEC;
(2)求AE的长;
(3)求二面角E—PC—A的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】砂糖橘是柑橘类的名优品种,因其味甜如砂糖故名.某果农选取一片山地种植砂糖橘,收获时,该果农随机选取果树20株作为样本测量它们每一株的果实产量(单位:kg),获得的所有数据按照区间(40,45],(45,50],(50,55],(55,60]进行分组,得到频率分布直方图如图所示.已知样本中产量在区间(45,50]上的果树株数是产量在区间(50,60]上的果树株数的![]() 倍.
倍.

(1)求a,b的值;
(2)从样本中产量在区间(50,60]上的果树里随机抽取两株,求产量在区间(55,60]上的果树至少有一株被抽中的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com