
【题目】已知直线l经过直线2x+y-5=0与x-2y=0的交点P.
(1)点A(5,0)到直线l的距离为3,求直线l的方程;
(2)求点A(5,0)到直线l的距离的最大值.
科目:高中数学 来源: 题型:
【题目】设函数f(x)=xex , 则( )
A.x=1为f(x)的极大值点
B.x=1为f(x)的极小值点
C.x=﹣1为f(x)的极大值点
D.x=﹣1为f(x)的极小值点
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学对高三学生进行体能测试,已知高三某文科班有学生30人,立定跳远的测试成绩用茎叶图表示如图(单位: ![]() );男生成绩在
);男生成绩在![]() 以上(包括
以上(包括![]() )定义为“合格”,成绩在
)定义为“合格”,成绩在![]() 以下(不包括
以下(不包括![]() )定义为“不合格”;女生成绩在
)定义为“不合格”;女生成绩在![]() 以上(包括
以上(包括![]() )定义为“合格”,成绩在
)定义为“合格”,成绩在![]() 以下(不包括
以下(不包括![]() )定义为“不合格.
)定义为“不合格.

(1)求女生立定跳远测试成绩的中位数;
(2)若在男生中按成绩是否合格进行分层抽样,抽取6人,求抽取成绩为“合格”的学生人数;
(3)若从(2)中抽取的6名男生中任意选取4人,求这4人中至少有3人“合格”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax+ ![]() ,其中函数f(x)的图象在点(1,f(1))处的切线方程为y=x﹣1.
,其中函数f(x)的图象在点(1,f(1))处的切线方程为y=x﹣1.
(1)若a= ![]() ,求函数f(x)的解析式;
,求函数f(x)的解析式;
(2)若f(x)≥g(x)在[1,+∞)上恒成立,求实数a的取值范围;
(3)证明:1+ ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在![]() 上的函数
上的函数![]() ,如果满足:对任意
,如果满足:对任意![]() ,存在常数
,存在常数![]() ,都有
,都有![]() 成立,则称
成立,则称![]() 是
是![]() 上的有界函数,其中
上的有界函数,其中![]() 称为函数
称为函数![]() 的上界.
的上界.
(![]() )判断函数
)判断函数![]() ,
, ![]() 是否是有界函数,请写出详细判断过程.
是否是有界函数,请写出详细判断过程.
(![]() )试证明:设
)试证明:设![]() ,
, ![]() ,若
,若![]() ,
, ![]() 在
在![]() 上分别以
上分别以![]() ,
, ![]() 为上界,求证:函数
为上界,求证:函数![]() 在
在![]() 上以
上以![]() 为上界.
为上界.
(![]() )若函数
)若函数![]() 在
在![]() 上是以
上是以![]() 为上界的有界函数,求实数
为上界的有界函数,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某车间为了规定工时定额,需要确定加工零件所花费的时间,为此进行了5次试验,收集数据如下:
加工零件x(个) | 10 | 20 | 30 | 40 | 50 |
加工时间y(分钟) | 64 | 69 | 75 | 82 | 90 |
经检验,这组样本数据具有线性相关关系,那么对于加工零件的个数x与加工时间y这两个变量,下列判断正确的是( )
A.成正相关,其回归直线经过点(30,75)
B.成正相关,其回归直线经过点(30,76)
C.成负相关,其回归直线经过点(30,76)
D.成负相关,其回归直线经过点(30,75)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】x,y 满足约束条件 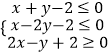 ,若 z=y﹣ax 取得最大值的最优解不唯一,则实数 a 的值为( )
,若 z=y﹣ax 取得最大值的最优解不唯一,则实数 a 的值为( )
A.![]() 或﹣1
或﹣1
B.2 或 ![]()
C.2 或1
D.2 或﹣1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com