
【题目】某海关对同时从![]() 三个不同地区进口的某种商品进行随机抽样检测,已知从
三个不同地区进口的某种商品进行随机抽样检测,已知从![]() 三个地区抽取的商品件数分别是50,150,100.检测人员再用分层抽样的方法从海关抽样的这些商品中随机抽取6件样品进行检测.
三个地区抽取的商品件数分别是50,150,100.检测人员再用分层抽样的方法从海关抽样的这些商品中随机抽取6件样品进行检测.
(1)求这6件样品中,来自![]() 各地区商品的数量;
各地区商品的数量;
(2)若在这6件样品中随机抽取2件送往另一机构进行进一步检测,求这2件样品来自相同地区的概率.
【答案】(1)1,3,2;(2) 这2件样品来自相同地区的概率是![]() .
.
【解析】试题分析:(1)由样本容量与总体中的个体数的比是![]() 可得,
可得, ![]() 三个地区抽到的商品数量分别是
三个地区抽到的商品数量分别是![]() ,
, ![]() ,
, ![]() .;(2)根据列举法得到在这
.;(2)根据列举法得到在这![]() 件样品中随机抽取
件样品中随机抽取![]() 件的基本事件总数,以及这
件的基本事件总数,以及这![]() 件商品来自相同地区的事件个数,代入古典概型概率计算公式,可得结果.
件商品来自相同地区的事件个数,代入古典概型概率计算公式,可得结果.
试题解析:(1)因为样本容量与总体中的个体数的比是![]()
所以, ![]() 三个地区抽到的商品数量分别是
三个地区抽到的商品数量分别是
![]() ,
, ![]() ,
, ![]() .
.
(2)记来自![]() 三个地区的6件样品分别为
三个地区的6件样品分别为
![]() ;
; ![]() ;
; ![]() ,
, ![]() ;
;
则从6件样品中抽取2件商品构成的所有基本事件为
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,共15个.
,共15个.
记“2件样品来自相同地区”为事件![]() ,这些基本事件共有4个,
,这些基本事件共有4个,
所以![]() ,即这2件样品来自相同地区的概率是
,即这2件样品来自相同地区的概率是![]() .
.


 字词句段篇系列答案
字词句段篇系列答案科目:高中数学 来源: 题型:
【题目】椭圆![]() 的离心率是
的离心率是![]() ,过点
,过点![]() 的动直线
的动直线![]() 与椭圆相交于
与椭圆相交于![]() 两点,当直线
两点,当直线![]() 与
与![]() 轴平行时,直线
轴平行时,直线![]() 被椭圆
被椭圆![]() 截得的线段长为
截得的线段长为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)在![]() 轴上是否存在异于点
轴上是否存在异于点![]() 的定点
的定点![]() ,使得直线
,使得直线![]() 变化时,总有
变化时,总有![]() ?若存在,求出点
?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知F1 , F2分别为椭圆C: ![]() +
+ ![]() =1(a>b>0)的左、右两个焦点,椭圆上点M(
=1(a>b>0)的左、右两个焦点,椭圆上点M( ![]() ,
, ![]() )到F1、F2两点的距离之和等于4.
)到F1、F2两点的距离之和等于4.
(1)求椭圆C的方程;
(2)已知过右焦点且垂直于x轴的直线与椭圆交于点N(点N在第一象限),E,F是椭圆C上的两个动点,如果kEN+KFN=0,证明直线EF的斜率为定值,并求出这个定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】BD是等腰直角三角形△ABC腰AC上的中线,AM⊥BD于点M,延长AM交BC于点N,AF⊥BC于点F,AF与BD交于点E.
(1)求证;△ABE≌△ACN;
(2)求证:∠ADB=∠CDN.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,我国许多省市雾霾天气频发,为增强市民的环境保护意识,某市面向全市征召![]() 名义务宣传志愿者,成立环境保护宣传组织,现把该组织的成员按年龄分成
名义务宣传志愿者,成立环境保护宣传组织,现把该组织的成员按年龄分成![]() 组第
组第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,得到的频率分布直方图如图所示,已知第
,得到的频率分布直方图如图所示,已知第![]() 组有
组有![]() 人.
人.

(1)求该组织的人数;
(2)若在第![]() 组中用分层抽样的方法抽取
组中用分层抽样的方法抽取![]() 名志愿者参加某社区的宣传活动,应从第
名志愿者参加某社区的宣传活动,应从第![]() 组各抽取多少名志愿者?
组各抽取多少名志愿者?
(3)在(2)的条件下,该组织决定在这![]() 名志愿者中随机抽取
名志愿者中随机抽取![]() 名志愿者介绍宣传经验,求第
名志愿者介绍宣传经验,求第![]() 组至少有
组至少有![]() 名志愿者被抽中的概率.
名志愿者被抽中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 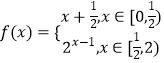 ,若存在x1 , x2 , 当0≤x1<x2<2时,f(x1)=f(x2),则x1f(x2)﹣f(x2)的取值范围为( )
,若存在x1 , x2 , 当0≤x1<x2<2时,f(x1)=f(x2),则x1f(x2)﹣f(x2)的取值范围为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业生产甲、乙两种产品,已知生产每吨甲产品要用A原料3吨,B原料2吨,生产每吨乙产品要用A原料1吨,B原料3吨。销售每吨甲产品可获得利润5万元,每吨乙产品可获得利润3万元,该企业在一个生产周期内消耗A原料不超过13吨,B原料不超过18吨,那么该企业可获得最大利润是___________万元
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方体ABCD-A1B1C1D1中,M、N、E、F分别是棱A1B1、A1D1、B1C1、C1D1的中点.
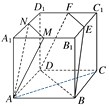
(1)求MN与AC所成角,并说明理由.
(2)求证:平面AMN∥平面EFDB.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com