
 名学生,他们每天自主学习的时间全部在
名学生,他们每天自主学习的时间全部在 分钟到
分钟到 分钟之间,按他们学习时间的长短分
分钟之间,按他们学习时间的长短分 个组统计,得到如下频率分布表:
个组统计,得到如下频率分布表:| 组别 | 分组 | 频数 | 频率 |
| 第一组 |  | |  |
| 第二组 |  |  |  |
| 第三组 |  |  |  |
| 第四组 |  |  |  |
| 第五组 |  | |  |
 ,
, 的值;
的值; 名学生中抽取
名学生中抽取 名进行研究,问应抽取多少名第一组的学生?
名进行研究,问应抽取多少名第一组的学生?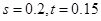 (2)
(2)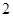 (3)
(3)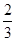
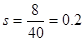 ,
,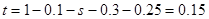 . 4分
. 4分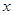 名第一组的学生,则
名第一组的学生,则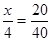
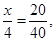 得
得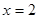 .
.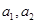 ,2名女生为
,2名女生为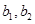 .
.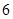 种结果,列举如下:
种结果,列举如下: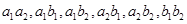 . 9分
. 9分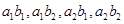 这4种结果, 10分
这4种结果, 10分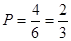 . 12分
. 12分

科目:高中数学 来源:不详 题型:解答题
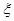 ,求随机变量
,求随机变量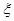 的分布列及数学期望.
的分布列及数学期望.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
A. | B. | C. | D. |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com