已知不等式sin2x+sinx+1<a 有解则a的范围为 .
【答案】
分析:由题意可得
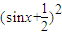
<a-

有解,再由
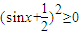
,得到a-

>0,从而求出a的范围.
解答:解:不等式sin
2x+sinx+1<a 有解,即
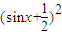
<a-

有解.
由于当sinx=-

时,
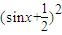
有最小值等于0; 当sinx=1时,
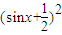
有最大值等于

,
∴0≤
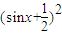
≤

.
要使
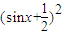
<a-

有解,a-

应大于
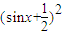
的最小值,
故 a-

>0,解得
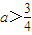
.
故答案为:
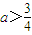
.
点评:本题主要考查正弦函数的定义域和值域,一元二次不等式的应用,由
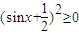
,得到a-

>0,是解题
的关键.
