
思路分析:先取n=1,2,3探求a,b,c的值,然后用数学归纳法证明对一切n∈N*,a,b,c所确定的等式都成立.
解:分别用n=1,2,3代入解方程组
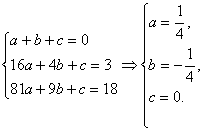
下面用数学归纳法证明.
(1)当n=1时,由上可知等式成立;
(2)假设当n=k时,等式成立,
则当n=k+1时,
左边=1·[(k+1)2-12]+2[(k+1)2-22]+…+k[(k+1)2-k2]+(k+1)[(k+1)2-(k+1)2]=1·(k2-12)+2(k2-22)+…+k(k2-k2)+1·(2k+1)+2(2k+1)+…+k(2k+1)
=![]() k4+(-
k4+(-![]() )k2+(2k+1)+2(2k+1)+…+k(2k+1)=
)k2+(2k+1)+2(2k+1)+…+k(2k+1)=![]() (k+1)4-
(k+1)4-![]() (k+1)2.
(k+1)2.
∴当n=k+1时,等式成立.
由(1)(2)得等式对一切的n∈N*均成立.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:高中数学 来源: 题型:
(1)求d和q.
(2)是否存在常数a,b,使对于一切n∈N+,都有an=logabn+b成立?若存在,求之;不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com