解:(Ⅰ)设A、B两点的坐标分别为A(x
1,y
1),B(x
2,y
2),
则由
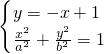
得:(a
2+b
2)x
2-2a
2x+a
2-a
2b
2=0,
由根与系数的关系,得

,
且判别式△=4a
2b
2(a
2+b
2-1)>0,即a
2+b
2-1>0(*);
∴线段AB的中点坐标为(

).
由已知得

,
∴a
2=2b
2=2(a
2-c
2),∴a
2=2c
2;故椭圆的离心率为

.
(Ⅱ)由(Ⅰ)知b=c,从而椭圆的右焦点坐标为F(b,0),
设F(b,0)关于直线l:x-2y=0的对称点为(x
0,y
0),
则

且

,
解得

.
由已知得 x
02+y
02=4,∴

,
∴b
2=4,代入(Ⅰ)中(*)满足条件
故所求的椭圆方程为
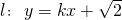
.
分析:(Ⅰ)设出A、B两点的坐标,由方程组
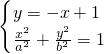
得关于x的一元二次方程;由根与系数的关系,可得x
1+x
2,y
1+y
2;从而得线段AB的中点坐标,代入直线l的方程x-2y=0,得出a、c的关系,从而求得椭圆的离心率.
(Ⅱ)设椭圆的右焦点坐标为F(b,0),F关于直线l:x-2y=0的对称点为(x
0,y
0),则由互为对称点的连线被对称轴垂直平分,可得方程组

,解得x
0、y
0;代入圆的方程 x
02+y
02=4,得出b的值,从而得椭圆的方程.
点评:本题考查了直线与椭圆的综合应用问题,也考查了一定的逻辑思维能力和计算能力;解题时应细心解答.

 相交于A、B两点,且线段AB的中点在直线l:x-2y=0上.
相交于A、B两点,且线段AB的中点在直线l:x-2y=0上.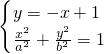 得:(a2+b2)x2-2a2x+a2-a2b2=0,
得:(a2+b2)x2-2a2x+a2-a2b2=0, ,
, ).
). ,
, .
. 且
且 ,
, .
. ,
,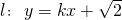 .
.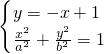 得关于x的一元二次方程;由根与系数的关系,可得x1+x2,y1+y2;从而得线段AB的中点坐标,代入直线l的方程x-2y=0,得出a、c的关系,从而求得椭圆的离心率.
得关于x的一元二次方程;由根与系数的关系,可得x1+x2,y1+y2;从而得线段AB的中点坐标,代入直线l的方程x-2y=0,得出a、c的关系,从而求得椭圆的离心率. ,解得x0、y0;代入圆的方程 x02+y02=4,得出b的值,从而得椭圆的方程.
,解得x0、y0;代入圆的方程 x02+y02=4,得出b的值,从而得椭圆的方程.

 名校课堂系列答案
名校课堂系列答案