
【题目】2019年12月,全国各中小学全体学生都参与了《禁毒知识》的答题竞赛,现从某校高一年级参加考试的学生中抽出60名学生,将其成绩(单位:分)整理后,得到如下频率分布直方图(其中分组区间为![]() ,
,![]() ,…
,…![]() ).
).
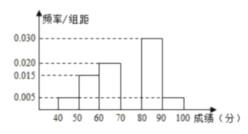
(1)求成绩在![]() 的频率,并补全此频率分布直方图;
的频率,并补全此频率分布直方图;
(2)求这次考试成绩的中位数的估计值;
(3)若从抽出的成绩在![]() 和
和![]() 的学生中任选两人,求他们的成绩在同一分组区间的概率.
的学生中任选两人,求他们的成绩在同一分组区间的概率.
【答案】(1)0.25;频率分布直方图见解析(2)74;(3)![]() .
.
【解析】
(1)根据频率之和等于![]() 公式即可求出成绩在
公式即可求出成绩在![]() 的频率.
的频率.
(2)先求前三组的频率之和为![]() ,前四组的频率之和为
,前四组的频率之和为![]() ,则中位数落在第四组,设中位数为
,则中位数落在第四组,设中位数为![]() ,根据公式
,根据公式![]() 即可求出中位数.
即可求出中位数.
(3)先算出成绩在![]() 和成绩在
和成绩在![]() 的人数,分别设为
的人数,分别设为![]() ,
,![]() ,
,![]() 和
和![]() ,
,![]() ,
,![]() ,再列举从中任选两人的结果和成绩在同一分组区间的结果,最后求概率即可.
,再列举从中任选两人的结果和成绩在同一分组区间的结果,最后求概率即可.
解:(1)第四小组的频率![]() .
.
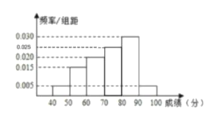
(2)第一组![]() 的频率
的频率![]() ,
,
第二组![]() 的频率
的频率![]() ,
,
第三组![]() 的频率
的频率![]() ,
,
第四组![]() 的频率
的频率![]()
前三组的频率之和为![]() ,前四组的频率之和为
,前四组的频率之和为![]() ,
,
所以中位数落在第四组,设中位数为![]() ,
,
则有:![]() ,∴
,∴![]() ,
,
所以这次考试成绩的中位数的估计值为74.
(3)由题意可知,成绩在![]() 的人数为
的人数为![]() ,
,
记他们分别为![]() ,
,![]() ,
,![]() ,成绩在
,成绩在![]() 的人数为
的人数为![]() ,
,
记他们分别为![]() ,
,![]() ,
,![]() ,
,
则从成绩在![]() 和
和![]() 的学生中任选两人的结果分别是:
的学生中任选两人的结果分别是:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 共15种,
共15种,
事件他们的成绩在同一分组区间的结果是:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,共6种,
,共6种,
所以所求事件的概率为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
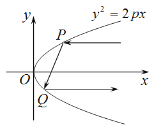
【题目】抛物线有如下光学性质:由其焦点射出的光线经抛物线反射后,沿平行于抛物线对称轴的方向射出.现有抛物线![]() ,如图一平行于
,如图一平行于![]() 轴的光线射向抛物线,经两次反射后沿平行
轴的光线射向抛物线,经两次反射后沿平行![]() 轴方向射出,若两平行光线间的最小距离为4,则该抛物线的方程为__________.
轴方向射出,若两平行光线间的最小距离为4,则该抛物线的方程为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列有关命题的说法错误的是( )
A.若“p∨q”为假命题,则p,q均为假命题
B.“x=1”是“x≥1”的充分不必要条件
C.“sinx=![]() ”的必要不充分条件是“x=
”的必要不充分条件是“x=![]() ”
”
D.若命题p:x0∈R,x02≥0,则命题¬p:x∈R,x2<0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】点![]() 、
、![]() 、
、![]() 分别是正方体
分别是正方体![]() 的棱
的棱![]() ,
,![]() ,
,![]() 的中点,则下列命题中的真命题是__________(写出所有真命题的序号).
的中点,则下列命题中的真命题是__________(写出所有真命题的序号).
①以正方体的顶点为顶点的三棱锥的四个面中最多可以四个面都是直角三角形;
②点![]() 在直线
在直线![]() 上运动时,总有
上运动时,总有![]() ;
;
③点![]() 在直线
在直线![]() 上运动时,三棱锥
上运动时,三棱锥![]() 的体积是定值;
的体积是定值;
④若![]() 是正方体的面
是正方体的面![]() ,(含边界)内一动点,且点
,(含边界)内一动点,且点![]() 到点
到点![]() 和
和![]() 的距离相等,则点
的距离相等,则点![]() 的轨迹是一条线段.
的轨迹是一条线段.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的个数是( )
①一组数据的标准差越大,则说明这组数据越集中;
②曲线![]() 与曲线
与曲线![]() 的焦距相等;
的焦距相等;
③在频率分布直方图中,估计的中位数左边和右边的直方图的面积相等;
④已知椭圆![]() ,过点
,过点![]() 作直线,当直线斜率为
作直线,当直线斜率为![]() 时,M刚好是直线被椭圆截得的弦AB的中点.
时,M刚好是直线被椭圆截得的弦AB的中点.
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】C反应蛋白(CRP)是机体受到微生物入侵或组织损伤等炎症性刺激时细胞合成的急性相蛋白,医学认为CRP值介于0-10mg/L为正常值.下面是某患者在治疗期间连续5天的检验报告单中CRP值(单位:mg/L)与治疗大数的统计数据:
治疗天数x | 1 | 2 | 3 | 4 | 5 |
CRP值y | 51 | 40 | 35 | 28 | 21 |
(1)若CRP值y与治疗数x只有线性相关关系试用最小乘法求出y关于x的线性回归方程,并估计该者至少需要治疗多少天CRP值可以回到正常水平;
(2)为均衡城乡保障待遇,统一保障范同和支付准,为多保人员提供公平的基本医疗保障.某市城乡医疗保险实施办法指出:门诊报销比例为50%;住院报销比例,A类医疗机构80%,B类医疗机构60%.若张华参加了城乡基本医疗保险,他因CRP偏高选择在医疗机构治疗,医生为张华提供了三种治疗方案:方案一:门诊治疗,预计每天诊疗费80元;方案二:住院治疗,A类医疗机构,入院检查需花费600元,预计每天诊疗费100元;方案三:住院治疗,B类医疗机构,入院检查需花费400元,预计每天诊疗费40元;若张华需要经过连续治疗n天![]() ,请你为张华选择最经济实惠的治疗方案.
,请你为张华选择最经济实惠的治疗方案.
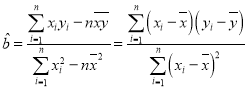 ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列五个命题:
①“![]() ”是“
”是“![]() 为R上的增函数”的充分不必要条件;
为R上的增函数”的充分不必要条件;
②函数![]() 有两个零点;
有两个零点;
③集合A={2,3},B={1,2,3},从A,B中各任意取一个数,则这两数之和等于4的概率是![]() ;
;
④动圆C即与定圆![]() 相外切,又与y轴相切,则圆心C的轨迹方程是
相外切,又与y轴相切,则圆心C的轨迹方程是![]()
⑤若对任意的正数x,不等式![]() 恒成立,则实数
恒成立,则实数![]() 的取值范围是
的取值范围是![]()
其中正确的命题序号是_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现要完成下列三项抽样调查:①从![]() 罐奶粉中抽取
罐奶粉中抽取![]() 罐进行食品安全卫生检查;②高二年级有
罐进行食品安全卫生检查;②高二年级有![]() 名学生,为调查学生的学习情况抽取一个容量为
名学生,为调查学生的学习情况抽取一个容量为![]() 的样本;③从某社区
的样本;③从某社区![]() 户高收入家庭,
户高收入家庭,![]() 户中等收入家庭,
户中等收入家庭,![]() 户低收入家庭中选出
户低收入家庭中选出![]() 户进行消费水平调查.以下各调查方法较为合理的是( )
户进行消费水平调查.以下各调查方法较为合理的是( )
A.①系统抽样,②简单随机抽样,③分层抽样
B.①简单随机抽样,②分层抽样,③系统抽样
C.①分层抽样,②系统抽样,③简单随机抽样
D.①简单随机抽样,②系统抽样,③分层抽样
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com