
【题目】函数![]() ,则
,则![]() 在
在![]() 的最大值
的最大值![]() ( )
( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
【答案】D
【解析】f′(x)=x![]() 2kx=x(
2kx=x(![]() 2k),
2k),
令f′(x)=0得x=0或x=ln2k,
令g(k)=kln2k,则g′(k)=1![]() <0
<0
∴g(k)在(![]() ,1]上是减函数,∴g(k)g(1)=1ln2>0,
,1]上是减函数,∴g(k)g(1)=1ln2>0,
∴k>ln2k,
∴f(x)在[0,ln2k]上单调递减,在(ln2k,k]上单调递增,
∴f(x)的最大值为f(0)或f(k).
f(k)f(0)=(k1)ekk3+1=(k1)(ekk2k1),
令h(x)=ekk2k1,则h′(k)=ek2k1,h′′(k)=ek2,
令h″(k)=0得k=ln2,
∴h′(k)在(![]() ,ln2)上单调递减,在(ln2,1]上单调递增,
,ln2)上单调递减,在(ln2,1]上单调递增,
∵h′(![]() )=
)=![]() 2<0,h′(1)=e3<0,
2<0,h′(1)=e3<0,
∴h′(k)<0在(![]() ,1]上恒成立,
,1]上恒成立,
∴h(k)在(![]() ,1]上是减函数,∴h(k)<h(
,1]上是减函数,∴h(k)<h(![]() )=
)=![]()
![]() <0,
<0,
∴f(k)f(0),
∴f(x)的最大值为f(k)=(k1)ekk3,
故选D.
方法 | 步骤 |
单调性法 | 先确定函数的单调性,再由单调性求最值 |
图象法 | 先作出函数的图象,再观察其最高点、最低点,求出最值 |
基本不等式法 | 先对解析式变形,使之具备“一正二定三相等”的条件后用基本不等式求出最值 |
导数法 | 先求导,然后求出在给定区间上的极值,最后结合端点值,求出最值 |
换元法 | 对比较复杂的函数可通过换元转化为熟悉的函数,再用相应的方法求最值 |


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:高中数学 来源: 题型:
【题目】“微信运动”已成为当下热门的运动方式,小王的微信朋友圈内也有大量好友参与了“微信运动”,他随机选取了其中的40人(男、女各20人),记录了他们某一天的走路步数,并将数据整理如下:
步数 性别 | 0-2000 | 2001-5000 | 5001-8000 | 8001-10000 | >10000 |
男 | 1 | 2 | 3 | 6 | 8 |
女 | 0 | 2 | 10 | 6 | 2 |
| 0.10 | 0.05 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
附: 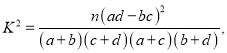
(1)已知某人一天的走路步数超过8000步被系统评定为“积极型”,否则为“懈怠型”,根据题意完成下面的 积极型 懈怠型 总计 男 女 总计 (2)若小王以这40位好友该日走路步数的频率分布来估计其所有微信好友每日走路步数的概率分布,现从小王的所有微信好友中任选2人,其中每日走路不超过5000步的有![]() 列联表,并据此判断能否有95%以上的把握认为“评定类型”与“性别”有关?
列联表,并据此判断能否有95%以上的把握认为“评定类型”与“性别”有关?![]() 人,超过10000步的有
人,超过10000步的有![]() 人,设
人,设![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知矩形![]() 所在平面垂直于直角梯形
所在平面垂直于直角梯形![]() 所在平面于直线
所在平面于直线![]() ,且
,且![]() ,
, ![]() 且
且![]() ∥
∥![]() .
.
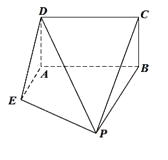
(Ⅰ)设点![]() 为棱
为棱![]() 中点,求证:
中点,求证: ![]() 平面
平面![]() ;
;
(Ⅱ)线段![]() 上是否存在一点
上是否存在一点![]() ,使得直线
,使得直线![]() 与平面
与平面![]() 所成角的正弦值等于
所成角的正弦值等于![]() ?若存在,试确定点
?若存在,试确定点![]() 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某单位的食堂中,食堂每天以10元/斤的价格购进米粉,然后以4.4元/碗的价格出售,每碗内含米粉0.2斤,如果当天卖不完,剩下的米粉以2元/斤的价格卖给养猪场.根据以往统计资料,得到食堂某天米粉需求量的频率分布直方图如图所示,若食堂购进了80斤米粉,以![]() (斤)(其中
(斤)(其中![]() )表示米粉的需求量,
)表示米粉的需求量, ![]() (元)表示利润.
(元)表示利润.
(1)估计该天食堂利润不少于760元的概率;
(2)在直方图的需求量分组中,以区间中间值作为该区间的需求量,以需求量落入该区间的频率作为需求量在该区间的概率,求![]() 的分布列和数学期望.
的分布列和数学期望.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2016·云南玉溪一中月考)已知函数![]() ,函数g(x)=f(x)-x+1的零点按从小到大的顺序排列成一个数列,该数列的前n项的和为Sn,则S10等于( )
,函数g(x)=f(x)-x+1的零点按从小到大的顺序排列成一个数列,该数列的前n项的和为Sn,则S10等于( )
A. 45 B. 55
C. 210-1 D. 29-1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的中点在原点,焦点在
的中点在原点,焦点在![]() 轴上,离心率
轴上,离心率![]() ,以两个焦点和短轴的两个端点为顶点的四边形的周长为8,面积为
,以两个焦点和短轴的两个端点为顶点的四边形的周长为8,面积为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过原点![]() 的两条直线
的两条直线![]() ,
, ![]() ,交椭圆
,交椭圆![]() 于
于![]() ,
, ![]() ,
, ![]() ,
, ![]() 四点,若
四点,若![]() ,求四边形
,求四边形![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知鸡的产蛋量与鸡舍的温度有关,为了确定下一个时段鸡舍的控制温度,某企业需要了解鸡舍的温度![]() (单位:
(单位:![]() ),对某种鸡的时段产蛋量
),对某种鸡的时段产蛋量![]() (单位:
(单位:![]() ) 和时段投入成本
) 和时段投入成本![]() (单位:万元)的影响,为此,该企业收集了7个鸡舍的时段控制温度
(单位:万元)的影响,为此,该企业收集了7个鸡舍的时段控制温度![]() 和产蛋量
和产蛋量![]() 的数据,对数据初步处理后得到了如图所示的散点图和表中的统计量的值.
的数据,对数据初步处理后得到了如图所示的散点图和表中的统计量的值.


其中![]() .
.
(1)根据散点图判断,![]() 与
与![]() 哪一个更适宜作为该种鸡的时段产蛋量
哪一个更适宜作为该种鸡的时段产蛋量![]() 关于鸡舍时段控制温度
关于鸡舍时段控制温度![]() 的回归方程类型?(给判断即可,不必说明理由)
的回归方程类型?(给判断即可,不必说明理由)
(2)若用![]() 作为回归方程模型,根据表中数据,建立
作为回归方程模型,根据表中数据,建立![]() 关于
关于![]() 的回归方程;
的回归方程;
(3)已知时段投入成本![]() 与
与![]() 的关系为
的关系为![]() ,当时段控制温度为
,当时段控制温度为![]() 时,鸡的时段产蛋量及时段投入成本的预报值分别是多少?
时,鸡的时段产蛋量及时段投入成本的预报值分别是多少?
附:①对于一组具有线性相关关系的数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为 ,
,![]() .
.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com