
 <ln(x+1)<x;
<ln(x+1)<x;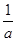 )为减,在(
)为减,在(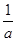 ,+
,+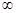 )为增
)为增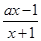 (x>-1,a>0)
(x>-1,a>0)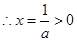
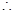 f(x)在(-1,
f(x)在(-1,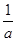 )为减,在(
)为减,在(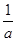 ,+
,+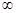 )为增 f (x)min=f(
)为增 f (x)min=f(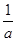 )=1-(a+1)ln(
)=1-(a+1)ln(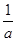 +1)
+1)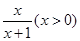
 F(x)在(0,+
F(x)在(0,+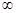 )为增函数
)为增函数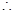 F(x)>0即
F(x)>0即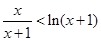
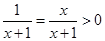
 G(x)在(0,+
G(x)在(0,+ )为增函数
)为增函数 G(x)>0即ln(x+1)<x
G(x)>0即ln(x+1)<x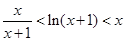
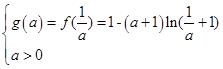
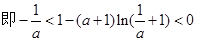


科目:高中数学 来源:不详 题型:解答题
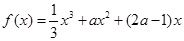 。
。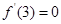 ,求a的值;
,求a的值;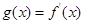 是偶函数,若过点A(1,m)
是偶函数,若过点A(1,m)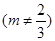 可作曲线y=f(x)的三条切线,求实数m的范围。
可作曲线y=f(x)的三条切线,求实数m的范围。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
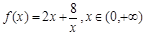 的最小值,并确定取得最小值时x的值.列表如下:
的最小值,并确定取得最小值时x的值.列表如下:| x | … | 0.5 | 1 | 1.5 | 1.7 | 1.9 | 2 | 2.1 | 2.2 | 2.3 | 3 | 4 | 5 | 7 | … |
| y | … | 16 | 10 | 8.34 | 8.1 | 8.01 | 8 | 8.01 | 8.04 | 8.08 | 8.6 | 10 | 11.6 | 15.14 | … |
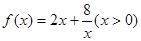 在区间(0,2)上递减;函数
在区间(0,2)上递减;函数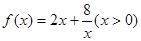 在区间 上递增.当
在区间 上递增.当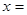 时,
时,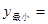 .
.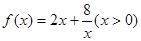 在区间(0,2)递减.
在区间(0,2)递减.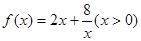 时,有最值吗?是最大值还是最小值?此时x为何值?(直接回答结果,不需证明)
时,有最值吗?是最大值还是最小值?此时x为何值?(直接回答结果,不需证明)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com