
设函数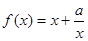 定义域为
定义域为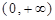 ,且
,且 .
.
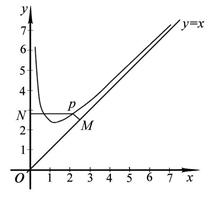
设点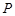 是函数图像上的任意一点,过点
是函数图像上的任意一点,过点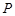 分别作直线
分别作直线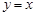 和
和 轴的垂线,垂足分别为
轴的垂线,垂足分别为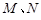 .
.
(1)写出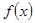 的单调递减区间(不必证明);(4分)
的单调递减区间(不必证明);(4分)
(2)问: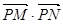 是否为定值?若是,则求出该定值,若不是,则说明理由;(7分)
是否为定值?若是,则求出该定值,若不是,则说明理由;(7分)
(3)设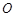 为坐标原点,求四边形
为坐标原点,求四边形 面积的最小值.(7分)
面积的最小值.(7分)
科目:高中数学 来源: 题型:解答题
(本题满分12分)
把边长为 的等边三角形铁皮剪去三个相同的四边形(如图阴影部分)后,用剩余部分做成一个无盖的正三棱柱形容器(不计接缝),设容器的高为
的等边三角形铁皮剪去三个相同的四边形(如图阴影部分)后,用剩余部分做成一个无盖的正三棱柱形容器(不计接缝),设容器的高为 ,容积为
,容积为 .
.
(Ⅰ)写出函数 的解析式,并求出函数的定义域;
的解析式,并求出函数的定义域;
(Ⅱ)求当x为多少时,容器的容积最大?并求出最大容积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com