
ЎѕМвДїЎїСфВнєН±оДћЈЁbienaoЈ©КЗЎ¶ѕЕХВЛгКхЎ¤ЙМ№¦Ў·Ап¶ФБЅЦЦЧ¶МеµДіЖОЅ.ИзНјЛщКѕЈ¬ИЎТ»ёці¤·ЅМеЈ¬°ґПВНјР±ёоТ»·ЦОЄ¶юЈ¬µГБЅёцДЈТ»СщµДИэАвЦщЈ¬іЖОЄЗµ¶ВЈЁИзНјЈ©.ФЩСШЖдЦРТ»ёцЗµ¶ВµДТ»ёц¶ҐµгУлПа¶ФµДАвЖКїЄЈ¬µГЛДАвЧ¶єНИэАвЧ¶ёчТ»ёцЈ¬УРТ»АвУлµЧГжґ№Ц±µДЛДАвЧ¶іЖОЄСфВнЈЁЛДАвЧ¶![]() Ј©УаПВИэАвЧ¶іЖОЄ±оДћЈЁИэАвЧ¶
Ј©УаПВИэАвЧ¶іЖОЄ±оДћЈЁИэАвЧ¶![]() Ј©ИфЅ«Діі¤·ЅМеСШЙПКцЗРёо·Ѕ·ЁµГµЅТ»ёцСфВнТ»ёц±оДћЈ¬ЗТёГСфВнµДХэКУНјєН±оДћµДІаКУНјИзНјЛщКѕЈ¬ФтїЙЗуіцёГСфВнєН±оДћµД±нГж»эЦ®єНОЄЈЁ Ј©
Ј©ИфЅ«Діі¤·ЅМеСШЙПКцЗРёо·Ѕ·ЁµГµЅТ»ёцСфВнТ»ёц±оДћЈ¬ЗТёГСфВнµДХэКУНјєН±оДћµДІаКУНјИзНјЛщКѕЈ¬ФтїЙЗуіцёГСфВнєН±оДћµД±нГж»эЦ®єНОЄЈЁ Ј©

A.![]() B.
B.![]()
C.![]() D.
D.![]()

| Дкј¶ | ёЯЦРїОіМ | Дкј¶ | іхЦРїОіМ |
| ёЯТ» | ёЯТ»Гв·СїОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СїОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СїОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СїОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СїОіМНЖјцЈЎ | іхИэ | іхИэГв·СїОіМНЖјцЈЎ |
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎї¶ЁТеФЪ![]() ЙПµДєЇКэ
ЙПµДєЇКэ![]() Ј¬ИфВъЧг:¶ФИОТв
Ј¬ИфВъЧг:¶ФИОТв![]() Ј¬ґжФЪіЈКэ
Ј¬ґжФЪіЈКэ![]() Ј¬¶јУР
Ј¬¶јУР![]() іЙБўЈ¬ФтіЖ
іЙБўЈ¬ФтіЖ![]() КЗ
КЗ![]() ЙПµДУРЅзєЇКэЈ¬ЖдЦР
ЙПµДУРЅзєЇКэЈ¬ЖдЦР![]() іЖОЄєЇКэ
іЖОЄєЇКэ![]() µДЙПЅз
µДЙПЅз
ЈЁ1Ј©Йи![]() Ј¬ЕР¶П
Ј¬ЕР¶П![]() ФЪ
ФЪ![]() ЙПКЗ·сКЗУРЅзєЇКэЈ¬ИфКЗЈ¬ЛµГчАнУЙЈ¬ІўРґіц
ЙПКЗ·сКЗУРЅзєЇКэЈ¬ИфКЗЈ¬ЛµГчАнУЙЈ¬ІўРґіц![]() ЛщУРЙПЅзµДЦµµДјЇєПЈ»ИфІ»КЗЈ¬ТІЗлЛµГчАнУЙ.
ЛщУРЙПЅзµДЦµµДјЇєПЈ»ИфІ»КЗЈ¬ТІЗлЛµГчАнУЙ.
ЈЁ2Ј©ИфєЇКэ![]() ФЪ
ФЪ![]() ЙПКЗТФ
ЙПКЗТФ![]() ОЄЙПЅзµДУРЅзєЇКэЈ¬ЗуКµКэ
ОЄЙПЅзµДУРЅзєЇКэЈ¬ЗуКµКэ![]() µДИЎЦµ·¶О§.
µДИЎЦµ·¶О§.
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
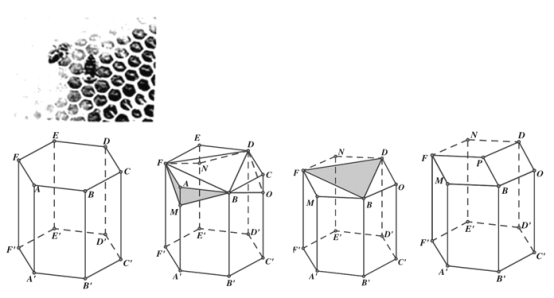
ЎѕМвДїЎї·діІКЗУЙ№¤·д·ЦГЪ·дАЇЅЁіЙµДґУХэГжїґЈ¬·діІїЪКЗУЙРн¶аХэБщ±ЯРОµДЦРїХЦщЧґМеБ¬ЅУ¶шіЙЈ¬ЦРїХЦщЧґМеµДµЧІїКЗУЙИэёцИ«µИµДБвРОГж№№іЙЈ¬БвРОµДТ»ёцЅЗ¶ИКЗ![]() Ј¬ХвСщµДЙијЖє¬УРЙоїМµДКэС§ФАнЎўОТ№ъЦшГыКэС§јТ»ЄВЮёэФшЧЁГЕСРѕї·діІµДЅб№№ЦшУРЎ¶МёМёУл·д·їЅб№№УР№ШµДКэС§ОКМвЎ·Ј®УГКэС§µДСЫ№вИҐїґ·діІµДЅб№№Ј¬ИзНјЈ¬ФЪБщАвЦщ
Ј¬ХвСщµДЙијЖє¬УРЙоїМµДКэС§ФАнЎўОТ№ъЦшГыКэС§јТ»ЄВЮёэФшЧЁГЕСРѕї·діІµДЅб№№ЦшУРЎ¶МёМёУл·д·їЅб№№УР№ШµДКэС§ОКМвЎ·Ј®УГКэС§µДСЫ№вИҐїґ·діІµДЅб№№Ј¬ИзНјЈ¬ФЪБщАвЦщ![]() µДИэёц¶ҐµгAЈ¬CЈ¬Eґ¦·Ц±рУГЖЅГжBFMЈ¬ЖЅГжBDOЈ¬ЖЅГжDFNЅШµфИэёцПаµИµДИэАвЧ¶
µДИэёц¶ҐµгAЈ¬CЈ¬Eґ¦·Ц±рУГЖЅГжBFMЈ¬ЖЅГжBDOЈ¬ЖЅГжDFNЅШµфИэёцПаµИµДИэАвЧ¶![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬ЖЅГжBFMЈ¬ЖЅГжBDOЈ¬ЖЅГжDFNЅ»УЪµгPЈ¬ѕНРОіЙБЛ·діІµДЅб№№Ј®ИзНјЈ¬ЙиЖЅГжPBODУлХэБщ±ЯРОµЧГжЛщіЙµД¶юГжЅЗµДґуРЎОЄ
Ј¬ЖЅГжBFMЈ¬ЖЅГжBDOЈ¬ЖЅГжDFNЅ»УЪµгPЈ¬ѕНРОіЙБЛ·діІµДЅб№№Ј®ИзНјЈ¬ЙиЖЅГжPBODУлХэБщ±ЯРОµЧГжЛщіЙµД¶юГжЅЗµДґуРЎОЄ![]() Ј¬ФтУРЈєЈЁ Ј©
Ј¬ФтУРЈєЈЁ Ј©
A.![]() B.
B.![]()
C.![]() D.ТФЙП¶јІ»¶Ф
D.ТФЙП¶јІ»¶Ф
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїЦ±ЅЗЧш±кПµxOyЦРЈ¬ТСЦЄMNКЗФІCЈє(x©Ѓ2)2+(y©Ѓ3)2=2µДТ»МхПТЈ¬ЗТCMЎНCNЈ¬PКЗMNµДЦРµг.µ±ПТMNФЪФІCЙПФЛ¶ЇК±Ј¬Ц±ПЯlЈєx©Ѓy©Ѓ5=0ЙПЧЬґжФЪБЅµгAЈ¬BЈ¬К№µГ![]() єгіЙБўЈ¬ФтПЯ¶ОABі¤¶ИµДЧоРЎЦµКЗ_____.
єгіЙБўЈ¬ФтПЯ¶ОABі¤¶ИµДЧоРЎЦµКЗ_____.
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїСфВнєН±оДћЈЁbienaoЈ©КЗЎ¶ѕЕХВЛгКхЎ¤ЙМ№¦Ў·Ап¶ФБЅЦЦЧ¶МеµДіЖОЅ.ИзНјЛщКѕЈ¬ИЎТ»ёці¤·ЅМеЈ¬°ґПВНјР±ёоТ»·ЦОЄ¶юЈ¬µГБЅёцДЈТ»СщµДИэАвЦщЈ¬іЖОЄЗµ¶ВЈЁИзНјЈ©.ФЩСШЖдЦРТ»ёцЗµ¶ВµДТ»ёц¶ҐµгУлПа¶ФµДАвЖКїЄЈ¬µГЛДАвЧ¶єНИэАвЧ¶ёчТ»ёцЈ¬УРТ»АвУлµЧГжґ№Ц±µДЛДАвЧ¶іЖОЄСфВнЈЁЛДАвЧ¶![]() Ј©УаПВИэАвЧ¶іЖОЄ±оДћЈЁИэАвЧ¶
Ј©УаПВИэАвЧ¶іЖОЄ±оДћЈЁИэАвЧ¶![]() Ј©ИфЅ«Діі¤·ЅМеСШЙПКцЗРёо·Ѕ·ЁµГµЅТ»ёцСфВнТ»ёц±оДћЈ¬ЗТёГСфВнµДХэКУНјєН±оДћµДІаКУНјИзНјЛщКѕЈ¬ФтїЙЗуіцёГСфВнєН±оДћµД±нГж»эЦ®єНОЄЈЁ Ј©
Ј©ИфЅ«Діі¤·ЅМеСШЙПКцЗРёо·Ѕ·ЁµГµЅТ»ёцСфВнТ»ёц±оДћЈ¬ЗТёГСфВнµДХэКУНјєН±оДћµДІаКУНјИзНјЛщКѕЈ¬ФтїЙЗуіцёГСфВнєН±оДћµД±нГж»эЦ®єНОЄЈЁ Ј©

A.![]() B.
B.![]()
C.![]() D.
D.![]()
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїГЙИХФІЙжј°µДКЗјёєОС§ЦРµДТ»ёцЦшГы¶ЁАнЈ¬ёГ¶ЁАнµДДЪИЭОЄЈєНЦФІЙПБЅМх»ҐПаґ№Ц±µДЗРПЯµДЅ»µг±ШФЪТ»ёцУлНЦФІН¬РДµДФІЙПЈ¬ёГФІіЖОЄФНЦФІµДГЙИХФІЈ¬ИфНЦФІ![]() µДГЙИХФІОЄ
µДГЙИХФІОЄ![]() Ј¬Фт
Ј¬Фт![]() ЈЁ Ј©
ЈЁ Ј©
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїИзНјЈ¬Хэ·ЅМе![]() µДАві¤ОЄ4Ј¬µгEЎўFОЄАвCDЎў
µДАві¤ОЄ4Ј¬µгEЎўFОЄАвCDЎў![]() µДЦРµг.
µДЦРµг.
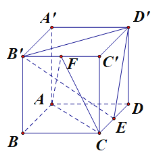
ЈЁ1Ј©ЗуЦ¤Јє![]() ЖЅГж
ЖЅГж![]() Ј»
Ј»
ЈЁ2Ј©ЗуЦ±ПЯ![]() УлЖЅГжACFЛщіЙЅЗµДХэПТЦµ.
УлЖЅГжACFЛщіЙЅЗµДХэПТЦµ.
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїТСЦЄНЦФІ![]() Јє
Јє![]() µДЧуЎўУТЅ№µгОЄ
µДЧуЎўУТЅ№µгОЄ![]() Ј¬
Ј¬![]() Ј¬ЙПЎўПВ¶ҐµгОЄ
Ј¬ЙПЎўПВ¶ҐµгОЄ![]() Ј¬
Ј¬![]() Ј¬ЛД±ЯРО
Ј¬ЛД±ЯРО![]() КЗГж»эОЄ2µДХэ·ЅРО.
КЗГж»эОЄ2µДХэ·ЅРО.
ЈЁ1Ј©ЗуНЦФІµД±кЧј·ЅіМЈ»
ЈЁ2Ј©ТСЦЄµг![]() Ј¬№эµг
Ј¬№эµг![]() µДЦ±ПЯ
µДЦ±ПЯ![]() УлНЦФІЅ»УЪ
УлНЦФІЅ»УЪ![]() Ј¬
Ј¬![]() БЅµгЈ¬ЗуЦ¤Јє
БЅµгЈ¬ЗуЦ¤Јє![]() .
.
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїёДёпїЄ·Е40¶аДкАґЈ¬іЗПзѕУГсЙъ»оґУЅвѕцОВ±ҐµДОпЦКРиЗуОЄЦчЦрЅҐЧЄ±дµЅёь¶аФЄ»ЇµДѕ«ЙсЧ·ЗуЈ¬Пы·СЅб№№ГчПФУЕ»Ї.ПВНјёшіцБЛ1983~2017ДкІї·ЦДк·ЭОТ№ъЕ©ґеѕУГсИЛѕщЙъ»оПы·СЦ§іцУл¶чёс¶ыПµКэЈЁ¶чёс¶ыПµКэКЗКіЖ·Ц§іцЧЬ¶оХјёцИЛПы·СЦ§іцЧЬ¶оµД±ИЦШЈ©НіјЖНј.¶ФЛщБРДк·ЭЅшРР·ЦОцЈ¬ФтПВБРЅбВЫґнОуµДКЗЈЁ Ј©
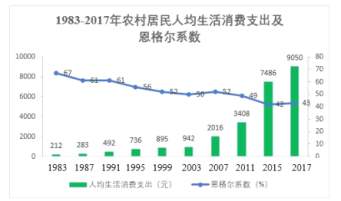
A.Е©ґеѕУГсИЛѕщЙъ»оПы·СЦ§іціКФці¤ЗчКЖ
B.Е©ґеѕУГсИЛѕщКіЖ·Ц§іцЧЬ¶оіКФці¤ЗчКЖ
C.2011ДкЦБ2015ДкЕ©ґеѕУГсИЛѕщЙъ»оПы·СЦ§іцФці¤Чоїм
D.2015ДкµЅ2017ДкЕ©ґеѕУГсИЛѕщЙъ»оПы·СЦ§іцФці¤±ИВКґуУЪИЛѕщКіЖ·Ц§іцЧЬ¶оФці¤±ИВК
Ійїґґр°ёєНЅвОц>>
°Щ¶ИЦВРЕ - Б·П°ІбБР±н - КФМвБР±н
єю±±КЎ»ҐБЄНшОҐ·ЁєНІ»БјРЕПўѕЩ±ЁЖЅМЁ | НшЙПУРє¦РЕПўѕЩ±ЁЧЁЗш | µзРЕХ©ЖѕЩ±ЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРє¦РЕПўѕЩ±ЁЧЁЗш | ЙжЖуЗЦИЁѕЩ±ЁЧЁЗш
ОҐ·ЁєНІ»БјРЕПўѕЩ±Ёµз»°Јє027-86699610 ѕЩ±ЁУКПдЈє58377363@163.com