
某高校在2013年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组,得到的频率分布表如图所示.
| 组号 | 分组 | 频数 | 频率 |
| 第1组 |  | 5 | 0.050 |
| 第2组 | 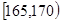 | ① | 0.350 |
| 第3组 |  | 30 | ② |
| 第4组 | 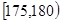 | 20 | 0.200 |
| 第5组 | 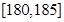 | 10 | 0.100 |
| 合计 | 100 | 1.00 | |

(1)①处的数据为35、②处的数据为0.300;(2)第3、4、5组分别抽取3人、2人、1人进入第二轮面试;(3)第4组的2位同学为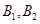 至少有一位同学入选的概率为
至少有一位同学入选的概率为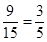 .
.
解析试题分析:(1)由频率=频数/总数可求得①、②两处的数据;(2)由分层抽样可以求得第3、4、5组分别抽取3人、2人、1人进入第二轮面试;(3)从六位同学中抽两位同学有15种可能,抽取的是第4组的2位同学有9种可能,所以第4组的2位同学至少有一位同学入选的概率为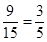 .
.
试题解析:(1)由题可知,
第2组的频数为 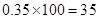 人, 1分
人, 1分
第3组的频率为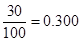 , 2分
, 2分
频率分布直方图如下: 2分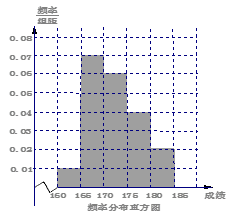
(2)因为第3、4、5组共有60名学生,所以
利用分层抽样在60名学生中抽取6名学生,每组分别为:
第3组: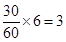 人, 6分
人, 6分
第4组: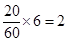 人, 7分
人, 7分
第5组: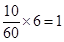 人, 8分
人, 8分
所以第3、4、5组分别抽取3人、2人、1人.
(3)设第3组的3位同学为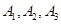 ,第4组的2位同学为
,第4组的2位同学为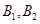 ,第5组的1位同学为
,第5组的1位同学为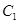 ,
,
则从六位同学中抽两位同学有15种可能如下: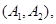
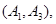
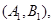

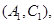

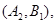
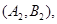
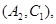
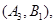
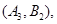
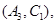
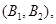
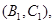
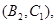 10分
10分
其中第4组的2位同学为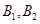 至少有一位同学入选的有:
至少有一位同学入选的有: 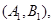

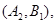
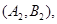
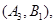
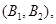
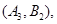
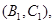
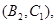
9中可能, 11分
所以其中第4组的2位同学为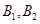 至少有一位同学入选的概率为
至少有一位同学入选的概率为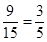 12分.
12分.
考点:概率、频率及抽样.


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:高中数学 来源: 题型:解答题
在某高校自主招生考试中,所有选报II类志向的考生全部参加了“数学与逻辑”和“阅读与表达”两个科目的考试,成绩分为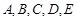 五个等级. 某考场考生的两科考试成绩数据统计如下图所示,其中“数学与逻辑”科目的成绩为
五个等级. 某考场考生的两科考试成绩数据统计如下图所示,其中“数学与逻辑”科目的成绩为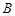 的考生有
的考生有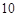 人.
人. 
(1)求该考场考生中“阅读与表达”科目中成绩为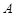 的人数;
的人数;
(2)若等级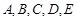 分别对应
分别对应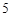 分,
分,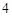 分,
分,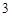 分,
分,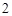 分,
分, 分,求该考场考生“数学与逻辑”科目的平均分;
分,求该考场考生“数学与逻辑”科目的平均分;
(3)已知参加本考场测试的考生中,恰有两人的两科成绩均为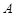 . 在至少一科成绩为
. 在至少一科成绩为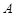 的考生中,随机抽取两人进行访谈,求这两人的两科成绩均为
的考生中,随机抽取两人进行访谈,求这两人的两科成绩均为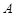 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在某次测验中,有6位同学的平均成绩为75分.用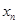 表示编号为
表示编号为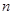 (
(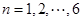 )的同学所得成绩,且前5位同学的成绩如下:70,76,72,70,72
)的同学所得成绩,且前5位同学的成绩如下:70,76,72,70,72
(1)求第6位同学的成绩 ,及这6位同学成绩的标准差
,及这6位同学成绩的标准差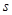 ;
;
(2)从前5位同学中,随机地选2位同学,求恰有1位同学成绩在区间(68,75)中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
为考查某种药物预防疾病的效果,进行动物试验,得到如下丢失数据的列联表:
| | 患病 | 未患病 | 总计 |
| 没服用药 | 20 | 30 | 50 |
| 服用药 | 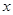 | 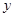 | 50 |
| 总计 | 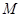 | 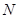 | 100 |
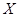 ;从服用药物的动物中任取两只,未患病数为
;从服用药物的动物中任取两只,未患病数为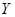 ,工作人员曾计算过
,工作人员曾计算过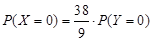 .
. 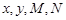 的值;
的值; 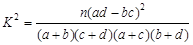 ,其中
,其中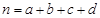 ;
; 、
、 有关联;
有关联; 、
、 有关联.
有关联.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
对甲、乙两名自行车赛手在相同条件下进行了6次测试,测得他们的最大速度(m/s)的数据如下表.
| 甲 | 27 | 38 | 30 | 37 | 35 | 31 |
| 乙 | 33 | 29 | 38 | 34 | 28 | 36 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某社团组织20名志愿者利用周末和节假日参加社会公益活动,志愿者中,年龄在20至40岁的有12人,年龄大于40岁的有8人.
(1)在志愿者中用分层抽样方法随机抽取5名,年龄大于40岁的应该抽取几名?
(2)上述抽取的5名志愿者中任取2名,求取出的2人中恰有1人年龄大于40岁的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
据《中国新闻网》10月21日报道,全国很多省市将英语考试作为高考改革的重点,一时间“英语考试该如何改”引起广泛关注.为了解某地区学生和包括老师、家长在内的社会人士对高考英语改革的看法,某媒体在该地区选择了3600人调查(若所选择的在校学生的人数低于被调查人群总数的80%,则认为本次调查“失效”),就“是否取消英语听力”的问题,调查统计的结果如下表:
| 应该取消 | 应该保留 | 无所谓 | ||
| 在校学生 | 2100人 | 120人 | y人 | ||
| 社会人士 | 600人 | x人 | z人 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某工厂有25周岁以上(含2S周岁)工人300名,25周岁以下工人200名为研究工人的日平均生产量是否与年龄有关,现采用分层抽样的方法,从中抽取了100名工人,先统计了他们某月的日平均生产件数,然后按工人年龄在“25周岁以上(含25周岁)”和“25周岁以下”分为两组,再将两组工人的日平均生产件数分成5组:[50,60), [60,70), [70,80), [80,90), [90,100), 分别加以统计,得到如图所示的频率分布直方图。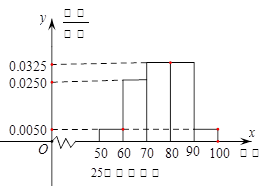
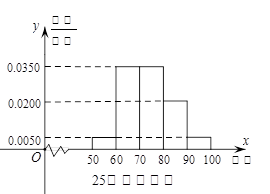
(1)求样本中“25周岁以上(含25周岁)组”抽取的人数、日生产量平均数;
(2)若“25周岁以上组”中日平均生产90件及90件以上的称为“生产能手”;“25周岁以下组”中日平均生产不足60件的称为“菜鸟”。从样本中的“生产能手”和”菜鸟”中任意抽取2人,求这2人日平均生产件数之和X的分布列及期望。(“生产能手”日平均生产件数视为95件,“菜鸟”日平均生产件数视为55件)。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在一次数学统考后,某班随机抽取10名同学的成绩进行样本分析,获得成绩数据的茎叶图如下.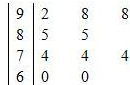
(Ⅰ)计算样本的平均成绩及方差;
(Ⅱ)现从80分以上的样本中随机抽出2名学生,求抽出的2名学生的成绩分别在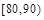 、
、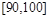 上的概率.
上的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com