
【题目】已知函数![]() .
.
(1)当![]() 时,求曲线
时,求曲线![]() 在
在![]() 处的切线方程;
处的切线方程;
(2)讨论![]() 的单调性;
的单调性;
(3)设过![]() 两点的直线的斜率为
两点的直线的斜率为![]() ,其中
,其中![]() 、
、![]() 为曲线
为曲线![]() 上的任意两点,并且
上的任意两点,并且![]() ,若
,若![]() 恒成立,证明:
恒成立,证明: ![]() .
.
【答案】(1)![]() (2)见解析(3)见解析
(2)见解析(3)见解析
【解析】试题分析:(1)由导数几何意义得切线斜率为![]() ,再根据点斜式求切线方程(2)因为导函数为
,再根据点斜式求切线方程(2)因为导函数为![]() ,所以根据
,所以根据![]() ,
, ![]() 讨论:
讨论: ![]() ,在
,在![]() 上递增;
上递增; ![]() 递增;
递增; ![]() 递减.(3)由(2)知
递减.(3)由(2)知![]() 的单调性,又
的单调性,又![]() ,所以由
,所以由![]() 恒成立得
恒成立得![]() ,利用斜率公式化简
,利用斜率公式化简![]() 得
得![]() ,转化为利用导数证明
,转化为利用导数证明![]() ,易证.
,易证.
试题解析:解:(1)当![]() 时,
时, ![]() ,
,
对函数![]() 求导得
求导得![]() ,
,
![]() ,又
,又![]() ,
,
![]() 曲线
曲线![]() 在
在![]() 处的切线方程为:
处的切线方程为: ![]() ;
;
(2)求导得![]() .
.
若![]() ,
, ![]() ,
, ![]() 在
在![]() 上递增;
上递增;
若![]() ,当
,当![]() 时,
时, ![]() ,
, ![]() 单调递增;
单调递增;
当![]() 时,
时, ![]() ,
, ![]() 单调递减.
单调递减.
(3)由(2)知,若![]() ,
, ![]() 在
在![]() 上递增,
上递增,
又![]() ,故
,故![]() 不恒成立.
不恒成立.
若![]() ,当
,当![]() 时,
时, ![]() 递减,
递减, ![]() ,不合题意.
,不合题意.
若![]() ,当
,当![]() 时,
时, ![]() 递增,
递增, ![]() ,不合题意.
,不合题意.
若![]() ,
, ![]() 在
在![]() 上递增,在
上递增,在![]() 上递减,
上递减,
![]() ,合题意.
,合题意.
故![]() ,且
,且![]() (当且仅当
(当且仅当![]() 时取“=”).
时取“=”).
设![]() ,
, 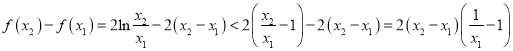
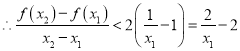 ,
,
因此, ![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知点A,B,C在圆x2+y2=1上运动,且AB⊥BC,若点P的坐标为 ![]() ,则
,则 ![]() 的取值范围为( )
的取值范围为( )
A.[8,10]
B.[9,11]
C.[8,11]
D.[9,12]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解春季昼夜温差大小与种子发芽多少之间的关系,现从4月的30天中随机挑选了5天进行研究,且分别记录了每天昼夜温差与每天每50颗种子浸泡后的发芽数,得到如下表格:
日期 | 4月1日 | 4月6日 | 4月12日 | 4月19日 | 4月27日 |
温差 | 2 | 3 | 5 | 4 | 1 |
发芽数 | 9 | 11 | 15 | 13 | 7 |
(1)从这5天中任选2天,记发芽的种子数分别为![]() ,求事件“
,求事件“![]() 均小于13”的概率;
均小于13”的概率;
(2)若4月30日昼夜温差为![]() ,请根据
,请根据![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() 估计该天种子浸泡后的发芽数.
估计该天种子浸泡后的发芽数.
参考公式:  ,
, ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com