
分析 利用椭圆的定义,求得|PF1|=3,|PF2|=1,则△PF2F1是直角三角形,即可求得△PF1F2的面积.
解答 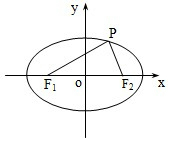 解:∵$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{2}$=1,焦点在x轴上,则a=2,由椭圆定义:|PF1|+|PF2|=4,丨F1F2丨=2c=2$\sqrt{2}$,
解:∵$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{2}$=1,焦点在x轴上,则a=2,由椭圆定义:|PF1|+|PF2|=4,丨F1F2丨=2c=2$\sqrt{2}$,
∵|PF1|-|PF2|=2,可得|PF1|=3,|PF2|=1,
由12+(2$\sqrt{2}$)2=9,
∴△PF2F1是直角三角形,
△PF1F2的面积$\frac{1}{2}$|PF2|×|F1F2|=$\frac{1}{2}$×1×2$\sqrt{2}$=$\sqrt{2}$.
故答案为:$\sqrt{2}$.
点评 本题考查椭圆的标准方程,椭圆的定义,考查计算能力,属于中档题.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:高中数学 来源: 题型:解答题
| 用水量(吨) | [0,10] | (10,20] | (20,30] | (30,40] | (40,50] | 合计 |
| 频数 | 200 | 400 | 200 | b | 100 | 1000 |
| 频率 | 0.2 | a | 0.2 | 0.1 | c | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,$\frac{3}{2}$+$\sqrt{2}$] | B. | (-∞,3] | C. | (-∞,6] | D. | (-∞,3+2$\sqrt{2}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 64π | B. | 65π | C. | 66π | D. | 128π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com