
【题目】已知点![]() 、
、![]() 、
、![]() 、
、![]() (
(![]() ),都在函数
),都在函数![]() (
(![]() ,
,![]() )的图像上;
)的图像上;
(1)若数列![]() 是等差数列,求证:数列
是等差数列,求证:数列![]() 是等比数列;
是等比数列;
(2)设![]() ,函数
,函数![]() 的反函数为
的反函数为![]() ,若函数
,若函数![]() 与函数
与函数![]() 的图像有公共点
的图像有公共点![]() ,求证:
,求证:![]() 在直线
在直线![]() 上;
上;
(3)设![]() ,
,![]() (
(![]() ),过点
),过点![]() 、
、![]() 的直线
的直线![]() 与两坐标轴围成的三角形面积为
与两坐标轴围成的三角形面积为![]() ,问:数列
,问:数列![]() 是否存在最大项?若存在,求出最大项的值,若不存在,请说明理由;
是否存在最大项?若存在,求出最大项的值,若不存在,请说明理由;
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:高中数学 来源: 题型:
【题目】已知数列![]() ,
,![]() 满足:
满足:![]() .
.
(1)若![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(2)若![]() ,且
,且![]() .
.
① 记![]() ,求证:数列
,求证:数列![]() 为等差数列;
为等差数列;
② 若数列![]() 中任意一项的值均未在该数列中重复出现无数次,求首项
中任意一项的值均未在该数列中重复出现无数次,求首项![]() 应满足的条件.
应满足的条件.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,对于任意
,对于任意![]() 满足
满足![]() ,且
,且![]() ,数列
,数列![]() 满足
满足![]() ,
,![]() ,其前
,其前![]() 项和为
项和为![]() .
.
(1)求数列![]() 、
、![]() 的通项公式;
的通项公式;
(2)令![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,求证:对于任意正整数
,求证:对于任意正整数![]() ,都有
,都有![]() ;
;
(3)将数列![]() 、
、![]() 的项按照“当
的项按照“当![]() 为奇数时,
为奇数时,![]() 放在前面”,“当
放在前面”,“当![]() 为偶数时,
为偶数时,![]() 放在前面”的要求进行“交叉排列”得到一个新的数列:
放在前面”的要求进行“交叉排列”得到一个新的数列:![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 求这个新数列的前
求这个新数列的前![]() 项和
项和![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(Ⅰ)若关于![]() 的不等式
的不等式![]() 在
在![]() 上恒成立,求
上恒成立,求![]() 的取值范围;
的取值范围;
(Ⅱ)设函数![]() ,在(Ⅰ)的条件下,试判断
,在(Ⅰ)的条件下,试判断![]() 在
在![]() 上是否存在极值.若存在,判断极值的正负;若不存在,请说明理由.
上是否存在极值.若存在,判断极值的正负;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 满足
满足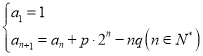 ,其中
,其中![]() .
.
(1)若数列前四项![]() ,
,![]() ,
,![]() ,
,![]() 依次成等差数列,求
依次成等差数列,求![]() ,
,![]() 的值;
的值;
(2)若![]() ,且数列
,且数列![]() 为等比数列,求
为等比数列,求![]() 的值;
的值;
(3)若![]() ,且
,且![]() 是数列
是数列![]() 的最小项,求
的最小项,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】垃圾分一分,城市美十分;垃圾分类,人人有责.某市为进一步推进生活垃圾分类工作,调动全民参与的积极性,举办了“垃圾分类游戏挑战赛”.据统计,在为期![]() 个月的活动中,共有
个月的活动中,共有![]() 万人次参与.为鼓励市民积极参与活动,市文明办随机抽取
万人次参与.为鼓励市民积极参与活动,市文明办随机抽取![]() 名参与该活动的网友,以他们单次游戏得分作为样本进行分析,由此得到如下频数分布表:
名参与该活动的网友,以他们单次游戏得分作为样本进行分析,由此得到如下频数分布表:
单次游戏得分 |
|
|
|
|
|
|
频数 |
|
|
|
|
|
|
(1)根据数据,估计参与活动的网友单次游戏得分的平均值及标准差(同一组中的数据用该组区间的中点值作代表);(其中标准差的计算结果要求精确到![]() )
)
(2)若要从单次游戏得分在![]() 、
、![]() 、
、![]() 的三组参与者中,用分层抽样的方法选取
的三组参与者中,用分层抽样的方法选取![]() 人进行电话回访,再从这
人进行电话回访,再从这![]() 人中任选
人中任选![]() 人赠送话费,求此
人赠送话费,求此![]() 人单次游戏得分不在同一组内的概率.
人单次游戏得分不在同一组内的概率.
附:![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】华东师大二附中乐东黄流中学位于我国南海边,有一片美丽的沙滩和一弯天然的海滨浴场.如图,海岸线MAN,![]() ,
,![]() (海岸线MAN上方是大海),现用长为BC的栏网围成一个三角形学生游泳场所,其中
(海岸线MAN上方是大海),现用长为BC的栏网围成一个三角形学生游泳场所,其中![]() .
.
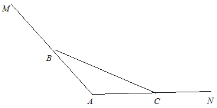
(1)若![]() ,求三角形游泳场所面积最大值;
,求三角形游泳场所面积最大值;
(2)若BC=600,![]() ,由于学生人数的增加需要扩大游泳场所面积,现在折线MBCN上方选点D,现用长为BD,DC的栏围成一个四边形游泳场所DBAC,使
,由于学生人数的增加需要扩大游泳场所面积,现在折线MBCN上方选点D,现用长为BD,DC的栏围成一个四边形游泳场所DBAC,使![]() ,求四边形游泳场所DBAC的最大面积.
,求四边形游泳场所DBAC的最大面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市对城市路网进行改造,拟在原有a个标段(注:一个标段是指一定长度的机动车道)的基础上,新建x个标段和n个道路交叉口,其中n与x满足n=ax+5.已知新建一个标段的造价为m万元,新建一个道路交叉口的造价是新建一个标段的造价的k倍.
(1)写出新建道路交叉口的总造价y(万元)与x的函数关系式;
(2)设P是新建标段的总造价与新建道路交叉口的总造价之比.若新建的标段数是原有标段数的20%,且k≥3.问:P能否大于![]() ,说明理由.
,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com