
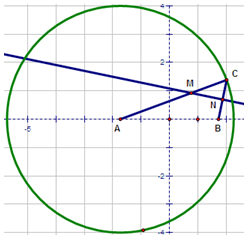
 以$A(-\sqrt{3},0)$为圆心,4为半径作圆,$B(\sqrt{3},0)$,C为圆上任意一点,分别连接AC,BC,过BC的中点N作BC的垂线,交AC于点M,当点C在圆上运动时,
以$A(-\sqrt{3},0)$为圆心,4为半径作圆,$B(\sqrt{3},0)$,C为圆上任意一点,分别连接AC,BC,过BC的中点N作BC的垂线,交AC于点M,当点C在圆上运动时,分析 (1)利用椭圆的定义求M点的轨迹方程,并说明它是何种曲线;
(2)直线y=kx+1代入椭圆方程,可得(1+4k2)x2+8kx=0,表示出弦长,即可求直线y=kx+1截(1)所得曲线弦长的最大值.
解答 解:(1)由题意,|MA|+|MB|=|AC|=4>2$\sqrt{3}$,
∴M点的轨迹是以A,B为焦点的椭圆,a=2,c=$\sqrt{3}$,
∴b=1,
∴椭圆方程为$\frac{{x}^{2}}{4}+{y}^{2}$=1;
(2)直线y=kx+1代入椭圆方程,可得(1+4k2)x2+8kx=0,
∴x=0或x=-$\frac{8k}{1+4{k}^{2}}$,
∴弦长L=$\sqrt{1+{k}^{2}}•|\frac{8k}{1+4{k}^{2}}|$,
设t=1+4k2(t≥1),则L2=-12($\frac{1}{t}$-$\frac{1}{3}$)2+$\frac{16}{3}$,
∴t=3时,L的最大值为$\frac{4\sqrt{3}}{3}$.
点评 本题考查轨迹方程,考查直线与椭圆的位置关系,考查弦长的计算,属于中档题.


 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | -2 | C. | -8 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\sqrt{2}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某电视台组织部分记者,用“10分制”随机调查某社区居民的幸福指数,现从调查人群中随机抽取16名,如图所示的茎叶图记录了他们的幸福指数的得分(以小数点的前一位数字为茎,小数点后的一位数字为叶):
某电视台组织部分记者,用“10分制”随机调查某社区居民的幸福指数,现从调查人群中随机抽取16名,如图所示的茎叶图记录了他们的幸福指数的得分(以小数点的前一位数字为茎,小数点后的一位数字为叶):查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com