
【题目】解答
(1)集合M={1,2,(m2﹣3m﹣1)+(m2﹣5m﹣6)i},N={3,﹣1},M∩N={3},求实数m的值.
(2)已知12= ![]() ×1×2×3,12+22=
×1×2×3,12+22= ![]() ×2×3×5,12+22+32=
×2×3×5,12+22+32= ![]() ×3×4×7,12+22+32+42=
×3×4×7,12+22+32+42= ![]() ×4×5×9,由此猜想12+22+…+n2(n∈N*)的表达式并用数学归纳法证明.
×4×5×9,由此猜想12+22+…+n2(n∈N*)的表达式并用数学归纳法证明.
【答案】
(1)解:由M={1,2,(m2﹣3m﹣1)+(m2﹣5m﹣6)i},N={3,﹣1},
且M∩N={3},
得(m2﹣3m﹣1)+(m2﹣5m﹣6)i=3,
所以,m2﹣3m﹣1=3且m2﹣5m﹣6=0,
解得m=﹣1;
(2)解:归纳猜想,得12+22+…+n2= ![]() (n∈N*);
(n∈N*);
证明:(1)当n=1时,12= ![]() ×1×2×3,猜想成立;
×1×2×3,猜想成立;
2)假设n=k(k≥1,且k∈N*)时,猜想成立,
即12+22+…+k2= ![]() ,
,
那么当n=k+1时,
12+22+…+k2= ![]() +(k+1)2
+(k+1)2
= ![]()
= ![]() ,(k∈N*),
,(k∈N*),
所以,当n=k+1时,猜想成立;
由(1)(2)可知,对任意的正整数n,猜想都成立
【解析】(1)根据交集的定义列出方程组,解方程组求出m的值;(2)归纳法猜想得出12+22+…+n2= ![]() (n∈N*),再用数学归纳法证明即可.
(n∈N*),再用数学归纳法证明即可.
【考点精析】解答此题的关键在于理解集合的交集运算的相关知识,掌握交集的性质:(1)A∩B![]() A,A∩B
A,A∩B![]() B,A∩A=A,A∩
B,A∩A=A,A∩![]() =
=![]() ,A∩B=B∩A;(2)若A∩B=A,则A
,A∩B=B∩A;(2)若A∩B=A,则A![]() B,反之也成立,以及对数学归纳法的定义的理解,了解数学归纳法是证明关于正整数n的命题的一种方法.
B,反之也成立,以及对数学归纳法的定义的理解,了解数学归纳法是证明关于正整数n的命题的一种方法.


 智慧小复习系列答案
智慧小复习系列答案科目:高中数学 来源: 题型:
【题目】已知定义在R上的函数y=f(x)对任意x都满足f(x+1)=﹣f(x),且当0≤x<1时,f(x)=x,则函数g(x)=f(x)﹣ln|x|的零点个数为个.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班级体育课举行了一次“投篮比赛”活动,为了了解本次投篮比赛学生总体情况,从中抽取了甲乙两个小组样本分数的茎叶图如图所示.
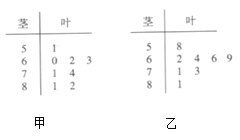
(1)分别求出甲乙两个小组成绩的平均数与方差,并判断哪一个小组的成绩更稳定:
(2)从甲组成绩不低于60分的同学中,任意抽取3名同学,设![]() 表示所抽取的3名同学中得分在
表示所抽取的3名同学中得分在![]() 的学生个数,求
的学生个数,求![]() 的分布列及其数学期望.
的分布列及其数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为直角坐标系的坐标原点,双曲线
为直角坐标系的坐标原点,双曲线![]()
![]() 上有一点
上有一点![]() (
(![]() ),点
),点![]() 在
在![]() 轴上的射影恰好是双曲线
轴上的射影恰好是双曲线![]() 的右焦点,过点
的右焦点,过点![]() 作双曲线
作双曲线![]() 两条渐近线的平行线,与两条渐近线的交点分别为
两条渐近线的平行线,与两条渐近线的交点分别为![]() ,
, ![]() ,若平行四边形
,若平行四边形![]() 的面积为1,则双曲线的标准方程是( )
的面积为1,则双曲线的标准方程是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. 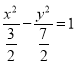
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】解答
(1)求证:函数y=x+ ![]() 有如下性质:如果常数a>0,那么该函数在(0,
有如下性质:如果常数a>0,那么该函数在(0, ![]() ]上是减函数,在[
]上是减函数,在[ ![]() ,+∞)上是增函数.
,+∞)上是增函数.
(2)若f(x)= ![]() ,x∈[0,1],利用上述性质,求函数f(x)的值域;
,x∈[0,1],利用上述性质,求函数f(x)的值域;
(3)对于(2)中的函数f(x)和函数g(x)=﹣x﹣2a,若对任意x1∈[0,1],总存在x2∈[0,1],使得g(x2)=f(x1),求实数a的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com