
 为奇函数,且当
为奇函数,且当 时,
时,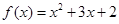 .当
.当 时,
时, 的最大值为
的最大值为 ,最小值为
,最小值为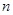 ,求
,求 的值.
的值. 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
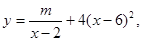 其中2<x<6,m为常数,已知销售价格为4元/件时,每月可售出21千件。(1)求m的值; (2)假设该淘宝店员工工资、办公等每月所有开销折合为每件2元(只考虑销售出的件数),试确定销售价格x的值,使该店每月销售饰品所获得的利润最大.(结果保留一位小数)
其中2<x<6,m为常数,已知销售价格为4元/件时,每月可售出21千件。(1)求m的值; (2)假设该淘宝店员工工资、办公等每月所有开销折合为每件2元(只考虑销售出的件数),试确定销售价格x的值,使该店每月销售饰品所获得的利润最大.(结果保留一位小数)查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.每个95元 | B.每个100元 | C.每个105元 | D.每个110元 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
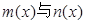 ,如果对于区间[a,b]中的任意x均有
,如果对于区间[a,b]中的任意x均有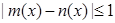 ,则称
,则称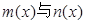 在[a,b]上是“密切函数”, [a,b]称为“密切区间”,若函数
在[a,b]上是“密切函数”, [a,b]称为“密切区间”,若函数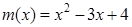 与
与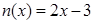 在区间[a,b]上是“密切函数”,则
在区间[a,b]上是“密切函数”,则 的最大值为 .
的最大值为 . 查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
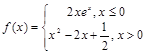 ,
,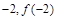 )的切线的斜率为
)的切线的斜率为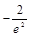
 的最小值为
的最小值为
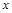 轴有4个交点
轴有4个交点 在
在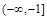 上为减函数,在
上为减函数,在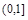 上也为减函数
上也为减函数查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com