【题目】三角形的面积为
，其中
，
，
为三角形的边长，
为三角形内切圆的半径，则利用类比推理，可得出四面体的体积为（ ）
A. 
B. 
C. 
，（
为四面体的高）
D. 
，（
，
，
，
分别为四面体的四个面的面积，
为四面体内切球的半径）
科目：高中数学 来源： 题型：
【题目】已知集合
，其中
，由
中的元素构成两个相应的集合：
， 
．
其中
是有序数对，集合
和
中的元素个数分别为
和
．
若对于任意的
，总有
，则称集合
具有性质
．
（Ⅰ）检验集合
与
是否具有性质
并对其中具有性质
的集合，写出相应的集合
和
．
（Ⅱ）对任何具有性质
的集合
，证明
．
（Ⅲ）判断
和
的大小关系，并证明你的结论．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，四棱锥
中，底面
为梯形， 
底面
， 
， 
， 
， 
．
（1）求证：平面
平面
；
（2）设
为
上的一点，满足
，若直线
与平面
所成角的正切值为
，求二面角
的余弦值．
查看答案和解析>>
科目：高中数学 来源： 题型：
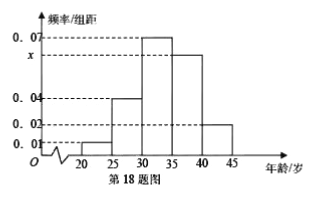
【题目】为增强市民的节能环保意识，汕头市面向全市征召义务宣传志愿者，从符合条件的 500 名志愿者中随机抽取 100 名，其年龄频率分布直方图如图所示，其中年龄分组区是：
，
(1)求图中
的值，并根据频率分布直方图估计这 500 名志愿者中年龄在
岁的人数；
(2)在抽出的 100 名志愿者中按年龄采用分层抽样的方法抽取 10 名参加人民广场的宣传活动，再从这 10 名志愿者中选取 3 名担任主要负责人．记这 3 名志愿者中“年龄低于 35 岁”的人数为 
，求
的分布列及数学期望.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】我国古代数学名著《算法统宗》中有如下问题：“远望巍巍塔七层，红光点点倍加增，共灯三百八十一，请问尖头几盏灯？”意思是：一座7层塔共挂了381盏灯，且相邻两层中的下一层灯数是上一层灯数的2倍，则塔的顶层共有灯（ ）
A. 1盏 B. 3盏 C. 5盏 D. 9盏
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某小区为了提高小区内人员的读书兴趣，特举办读书活动，准备进一定量的书籍丰富小区图书站，由于不同年龄段需要看不同类型的书籍，为了合理配备资源，现对小区看书人员进行年龄调查，随机抽取了一天40名读书者进行调查，将他们的年龄分成6段： 
， 
， 
， 
， 
， 
后得到如图所示的频率分布直方图，问：
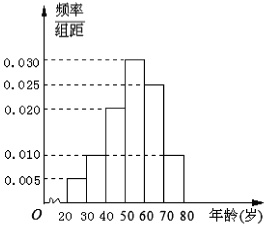
(1)在40名读书者中年龄分布在
的人数；
(2)估计40名读书者年龄的平均数和中位数；
(3)若从年龄在
的读书者中任取2名，求这两名读书者年龄在
的人数
的分布列和数学期望.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知鸡的产蛋量与鸡舍的温度有关，为了确定下一个时段鸡舍的控制温度，某企业需要了解鸡舍的温度
（单位：℃），对某种鸡的时段产蛋量
（单位： 
）和时段投入成本
（单位：万元）的影响，为此，该企业收集了7个鸡舍的时段控制温度
和产蛋量
的数据，对数据初步处理后得到了如图所示的散点图和表中的统计量的值．
|
|
|
|
|
|
|
17.40 | 82.30 | 3.6 | 140 | 9.7 | 2935.1 | 35.0 |
其中
.
（1）根据散点图判断， 
与
哪一个更适宜作为该种鸡的时段产蛋量
关于鸡舍时段控制温度
的回归方程类型？（给判断即可，不必说明理由）
（2）若用
作为回归方程模型，根据表中数据，建立
关于
的回归方程；
（3）已知时段投入成本
与
的关系为
，当时段控制温度为28℃时，鸡的时段产蛋量及时段投入成本的预报值分别是多少？
附：①对于一组具有有线性相关关系的数据
，其回归直线
的斜率和截距的最小二乘估计分别为
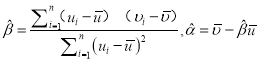
②
|
|
|
|
|
0.08 | 0.47 | 2.72 | 20.09 | 1096.63 |
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知圆锥曲线
(
是参数)和定点
,
、
是圆锥曲线的左、右焦点．
(1)求经过点
且垂直于直线
的直线
的参数方程；
(2)以坐标原点为极点， 
轴的正半轴为极轴建立极坐标系，求直线
的极坐标方程．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
