
【题目】记等比数列{an}前n项和为Sn , 已知a1+a3=30,3S1 , 2S2 , S3成等差数列.
(1)求数列{an}的通项公式;
(2)若数列{bn}满足b1=3,bn+1﹣3bn=3an , 求数列{bn}的前n项和Bn;
(3)删除数列{an}中的第3项,第6项,第9项,…,第3n项,余下的项按原来的顺序组成一个新数列,记为{cn},{cn}的前n项和为Tn , 若对任意n∈N* , 都有 ![]() >a,试求实数a的最大值.
>a,试求实数a的最大值.
【答案】
(1)解:设等比数列{an}的公比为q,∵a1+a3=30,3S1,2S2,S3成等差数列,
∴ ![]() =30,3S1+S3=2×2S2,化为:3a2=a3,解得q=3,a1=3.∴an=3n.
=30,3S1+S3=2×2S2,化为:3a2=a3,解得q=3,a1=3.∴an=3n.
(2)解:∵bn+1﹣3bn=3an=3n+1,∴ ![]() ﹣
﹣ ![]() =1.
=1.
∴数列 ![]() 是等差数列,公差为1,首项为1.
是等差数列,公差为1,首项为1.
∴ ![]() =1+(n﹣1)=n,∴bn=n3n.
=1+(n﹣1)=n,∴bn=n3n.
∴数列{bn}的前n项和Bn=3+2×32+…+n3n,
3Bn=32+2×33+…+(n﹣1)3n+n3n+1,
∴﹣2Bn=3+32+…+3n﹣n3n+1= ![]() ﹣n3n+1=
﹣n3n+1= ![]() 3n+1﹣
3n+1﹣ ![]() ,
,
∴Bn= ![]() ×3n+1+
×3n+1+ ![]()
(3)解:由题意可得:c2n﹣1=a3n﹣2=33n﹣2,c2n=a3n﹣1=33n﹣1,
∴n=2k(k∈N*)时,c2n﹣1+c2n=33n﹣2+33n﹣1= ![]() ×27n.
×27n.
Tn=T2k= ![]() ×
× ![]() =
= ![]() .
.
n=2k﹣1时,Tn=T2k﹣1=T2k﹣33n﹣1= ![]() ﹣33n﹣1=
﹣33n﹣1= ![]() .
.
因此:n=2k(k∈N*)时, ![]() =
= 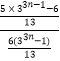 =
= ![]() +
+ ∈
![]() .
.
n=2k﹣1(k∈N*)时, ![]() =
= 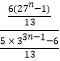 =
= ![]() ∈
∈ ![]() .
.
综上可得: ![]() >
> ![]() .∴a的最大值为
.∴a的最大值为 ![]()
【解析】(1)由a1+a3=30,3S1 , 2S2 , S3成等差数列,可得 ![]() =30,3S1+S3=2×2S2 , 化简解出利用等比数列的通项公式即可得出.(2)由bn+1﹣3bn=3an=3n+1 , 变形为
=30,3S1+S3=2×2S2 , 化简解出利用等比数列的通项公式即可得出.(2)由bn+1﹣3bn=3an=3n+1 , 变形为 ![]() ﹣
﹣ ![]() =1,利用等差数列的通项公式可得bn , 再利用“错位相减法”与等比数列的求和公式可得Bn . (3)由题意可得:c2n﹣1=a3n﹣2=33n﹣2 , c2n=a3n﹣1=33n﹣1 , 可得c2n﹣1+c2n=33n﹣2+33n﹣1=
=1,利用等差数列的通项公式可得bn , 再利用“错位相减法”与等比数列的求和公式可得Bn . (3)由题意可得:c2n﹣1=a3n﹣2=33n﹣2 , c2n=a3n﹣1=33n﹣1 , 可得c2n﹣1+c2n=33n﹣2+33n﹣1= ![]() ×27n . 对n分类讨论即可得出.
×27n . 对n分类讨论即可得出.
【考点精析】通过灵活运用等比数列的通项公式(及其变式)和数列的前n项和,掌握通项公式:![]() ;数列{an}的前n项和sn与通项an的关系
;数列{an}的前n项和sn与通项an的关系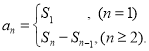 即可以解答此题.
即可以解答此题.


 53随堂测系列答案
53随堂测系列答案科目:高中数学 来源: 题型:
【题目】已知抛物线的方程为![]() ,过点
,过点![]() 的一条直线与抛物线
的一条直线与抛物线![]() 交于
交于![]() 两点,若抛物线在
两点,若抛物线在![]() 两点的切线交于点
两点的切线交于点![]() .
.
(1)求点![]() 的轨迹方程;
的轨迹方程;
(2)设直线![]() 与直线
与直线![]() 的夹角为
的夹角为![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}满足:a4=7,a10=19,其前n项和为Sn .
(1)求数列{an}的通项公式an及Sn;
(2)若等比数列{bn}的前n项和为Tn , 且b1=2,b4=S4 , 求Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知点A(2,4),直线l:x﹣2y+1=0.
(1)求过点A且平行于l的直线的方程;
(2)若点M在直线l上,且AM⊥l,求点M的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本题满分16分)
设函数![]() .
.
(1)若![]() =1时,函数
=1时,函数![]() 取最小值,求实数
取最小值,求实数![]() 的值;
的值;
(2)若函数![]() 在定义域上是单调函数,求实数
在定义域上是单调函数,求实数![]() 的取值范围;
的取值范围;
(3)若![]() ,证明对任意正整数
,证明对任意正整数![]() ,不等式
,不等式![]() 都成立.
都成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若 ![]() ,
, ![]() ,
, ![]() 为同一平面内互不共线的三个单位向量,并满足
为同一平面内互不共线的三个单位向量,并满足 ![]() +
+ ![]() +
+ ![]() =
= ![]() ,且向量
,且向量 ![]() =x
=x ![]() +
+ ![]()
![]() +(x+
+(x+ ![]() )
) ![]() (x∈R,x≠0,n∈N+).
(x∈R,x≠0,n∈N+).
(1)求 ![]() 与
与 ![]() 所成角的大小;
所成角的大小;
(2)记f(x)=| ![]() |,试求f(x)的单调区间及最小值.
|,试求f(x)的单调区间及最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋中有外形、质量完全相同的红球、黑球、黄球、绿球共12个.从中任取一球,得到红球的概率是 ![]() ,得到黑球或黄球的概率是
,得到黑球或黄球的概率是 ![]() ,得到黄球或绿球的概率也是
,得到黄球或绿球的概率也是 ![]() .
.
(1)试分别求得到黑球、黄球、绿球的概率;
(2)从中任取一球,求得到的不是“红球或绿球”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数f(x),若存在x0∈R,使f(x0)=x0成立,则称x0为f(x)的不动点.已知f(x)=ax2+(b+1)x+b﹣1(a≠0).
(1)当a=1,b=﹣2时,求函数f(x)的不动点;
(2)若对任意实数b,函数f(x)恒有两个相异的不动点,求a的范围;
(3)在(2)的条件下,若y=f(x)图象上A、B两点的横坐标是函数f(x)的不动点,且A、B两点关于直线y=kx+ ![]() 对称,求b的最小值.
对称,求b的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com