
【题目】为实现有效利用扶贫资金,增加贫困村民的收入,扶贫工作组结合某贫困村水质优良的特点,决定利用扶贫资金从外地购买甲、乙、丙三种鱼苗在鱼塘中进行养殖试验,试验后选择其中一种进行大面积养殖,已知鱼苗甲的自然成活率为0.8.鱼苗乙,丙的自然成活率均为0.9,且甲、乙、丙三种鱼苗是否成活相互独立.
(1)试验时从甲、乙,丙三种鱼苗中各取一尾,记自然成活的尾数为![]() ,求
,求![]() 的分布列和数学期望;
的分布列和数学期望;
(2)试验后发现乙种鱼苗较好,扶贫工作组决定购买![]() 尾乙种鱼苗进行大面积养殖,为提高鱼苗的成活率,工作组采取增氧措施,该措施实施对能够自然成活的鱼苗不产生影响.使不能自然成活的鱼苗的成活率提高了50%.若每尾乙种鱼苗最终成活后可获利10元,不成活则亏损2元,且扶贫工作组的扶贫目标是获利不低于37.6万元,问需至少购买多少尾乙种鱼苗?
尾乙种鱼苗进行大面积养殖,为提高鱼苗的成活率,工作组采取增氧措施,该措施实施对能够自然成活的鱼苗不产生影响.使不能自然成活的鱼苗的成活率提高了50%.若每尾乙种鱼苗最终成活后可获利10元,不成活则亏损2元,且扶贫工作组的扶贫目标是获利不低于37.6万元,问需至少购买多少尾乙种鱼苗?
【答案】(1)分布列见解析,2.6(2)40000尾
【解析】
(1)由题意得随机变量![]() 的所有可能取值为0,1,2,3,利用相互独立事件同时发生的概率,可计算
的所有可能取值为0,1,2,3,利用相互独立事件同时发生的概率,可计算![]() 的值,进而得到分布列和期望;
的值,进而得到分布列和期望;
(2)依题意知一尾乙种鱼苗最终成活的概率为![]() ,计算一尾乙种鱼苗的平均收益,进而计算
,计算一尾乙种鱼苗的平均收益,进而计算![]() 尾乙种鱼苗最终可获得的利润,再解不等式,即可得答案.
尾乙种鱼苗最终可获得的利润,再解不等式,即可得答案.
(1)记随机变量![]() 的所有可能取值为0,1,2,3,
的所有可能取值为0,1,2,3,
则![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
故![]() 的分布列为
的分布列为
| 0 | 1 | 2 | 3 |
| 0.002 | 0.044 | 0.306 | 0.648 |
![]() .
.
(2)根据已知乙种鱼苗自然成活的概率为0.9,
依题意知一尾乙种鱼苗最终成活的概率为![]() ,
,
所以一尾乙种鱼苗的平均收益为![]() 元.
元.
设购买![]() 尾乙种鱼苗,
尾乙种鱼苗,![]() 为购买
为购买![]() 尾乙种鱼苗最终可获得的利润,
尾乙种鱼苗最终可获得的利润,
则![]() ,解得
,解得![]() .
.
所以需至少购买40000尾乙种鱼苗,才能确保获利不低于37.6万元.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】某连锁餐厅新店开业,打算举办一次食品交易会,招待新老顾客试吃.项目经理通过查阅最近![]() 次食品交易会参会人数
次食品交易会参会人数![]() (万人)与餐厅所用原材料数量
(万人)与餐厅所用原材料数量![]() (袋),得到如下统计表:
(袋),得到如下统计表:
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | |
参会人数(万人) |
|
|
|
|
|
原材料(袋) |
|
|
|
|
|
(1)根据所给![]() 组数据,求出
组数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)已知购买原材料的费用![]() (元)与数量
(元)与数量![]() (袋)的关系为
(袋)的关系为![]() ,投入使用的每袋原材料相应的销售收入为
,投入使用的每袋原材料相应的销售收入为![]() 元,多余的原材料只能无偿返还,据悉本次交易大会大约有
元,多余的原材料只能无偿返还,据悉本次交易大会大约有![]() 万人参加,根据(1)中求出的线性回归方程,预测餐厅应购买多少袋原材料,才能获得最大利润,最大利润是多少?(注:利润
万人参加,根据(1)中求出的线性回归方程,预测餐厅应购买多少袋原材料,才能获得最大利润,最大利润是多少?(注:利润![]() 销售收入
销售收入![]() 原材料费用).
原材料费用).
参考公式: ,
,![]() .
.
参考数据:![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,要利用一半径为![]() 的圆形纸片制作三棱锥形包装盒.已知该纸片的圆心为
的圆形纸片制作三棱锥形包装盒.已知该纸片的圆心为![]() ,先以
,先以![]() 为中心作边长为
为中心作边长为![]() (单位:
(单位:![]() )的等边三角形
)的等边三角形![]() ,再分别在圆
,再分别在圆![]() 上取三个点
上取三个点![]() ,
,![]() ,
,![]() ,使
,使![]() ,
,![]() ,
,![]() 分别是以
分别是以![]() ,
,![]() ,
,![]() 为底边的等腰三角形.沿虚线剪开后,分别以
为底边的等腰三角形.沿虚线剪开后,分别以![]() ,
,![]() ,
,![]() 为折痕折起
为折痕折起![]() ,
,![]() ,
,![]() ,使得
,使得![]() ,
,![]() ,
,![]() 重合于点
重合于点![]() ,即可得到正三棱锥
,即可得到正三棱锥![]() .
.
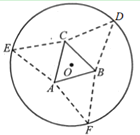

(1)若三棱锥![]() 是正四面体,求
是正四面体,求![]() 的值;
的值;
(2)求三棱锥![]() 的体积
的体积![]() 的最大值,并指出相应
的最大值,并指出相应![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某小区为了加强对“新型冠状病毒”的防控,确保居民在小区封闭期间生活不受影响,小区超市采取有力措施保障居民正常生活物资供应.为做好甲类生活物资的供应,超市对社区居民户每天对甲类生活物资的购买量进行了调查,得到了以下频率分布直方图.
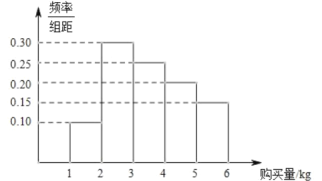
(1)从小区超市某天购买甲类生活物资的居民户中任意选取5户.
①若将频率视为概率,求至少有两户购买量在![]() (单位:
(单位:![]() )的概率是多少?
)的概率是多少?
②若抽取的5户中购买量在![]() (单位:
(单位:![]() )的户数为2户,从5户中选出3户进行生活情况调查,记3户中需求量在
)的户数为2户,从5户中选出3户进行生活情况调查,记3户中需求量在![]() (单位:
(单位:![]() )的户数为
)的户数为![]() ,求
,求![]() 的分布列和期望;
的分布列和期望;
(2)将某户某天购买甲类生活物资的量与平均购买量比较,当超出平均购买量不少于![]() 时,则称该居民户称为“迫切需求户”,若从小区随机抽取10户,且抽到k户为“迫切需求户”的可能性最大,试求k的值.
时,则称该居民户称为“迫切需求户”,若从小区随机抽取10户,且抽到k户为“迫切需求户”的可能性最大,试求k的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn,a1=1,an>0,Sn2=an+12﹣λSn+1,其中λ为常数.
(1)证明:Sn+1=2Sn+λ;
(2)是否存在实数λ,使得数列{an}为等比数列,若存在,求出λ;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三棱锥![]() (如图一)的平面展开图(如图二)中,四边形
(如图一)的平面展开图(如图二)中,四边形![]() 为边长等于
为边长等于![]() 的正方形,
的正方形,![]() 和
和![]() 均为正三角形,在三棱锥
均为正三角形,在三棱锥![]() 中:
中:
(I)证明:平面![]() 平面
平面![]() ;
;
(Ⅱ)若点![]() 在棱
在棱![]() 上运动,当直线
上运动,当直线![]() 与平面
与平面![]() 所成的角最大时,求二面角
所成的角最大时,求二面角![]() 的余弦值.
的余弦值.
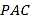
图一
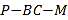
图二
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知离心率为![]() 的椭圆
的椭圆![]() 的左顶点为
的左顶点为![]() ,左焦点为
,左焦点为![]() ,及点
,及点![]() ,且
,且![]() 、
、![]() 、
、![]() 成等比数列.
成等比数列.
(1)求椭圆![]() 的方程;
的方程;
(2)斜率不为![]() 的动直线
的动直线![]() 过点
过点![]() 且与椭圆
且与椭圆![]() 相交于
相交于![]() 、
、![]() 两点,记
两点,记![]() ,线段
,线段![]() 上的点
上的点![]() 满足
满足![]() ,试求
,试求![]() (
(![]() 为坐标原点)面积的取值范围.
为坐标原点)面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为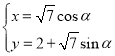 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的极坐标方程和
的极坐标方程和![]() 的直角坐标方程;
的直角坐标方程;
(2)直线![]() 与曲线
与曲线![]() ,
,![]() 分別交于第一象限内
分別交于第一象限内![]() ,
,![]() 两点,求
两点,求![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com