
分析 (1)先求出f(x+2)的解析式,根据函数的奇偶性,求出a的值即可;
(2)求出P-Q的表达式,变形整理成完全平方式,从而判断出结论;
(3)先求出函数的对称轴,通过讨论对称轴的位置,从而判断出函数的单调性,得到函数的最小值的表达式,解出a的值即可.
解答 解:(1)f(x+2)=(x+2)2+(4-2a)(x+2)+a2+1
=x2+(8-2a)x+a2-4a+13,
若f(x+2)是偶函数,则8-2a=0,解得:a=4;
(2)P-Q=$\frac{1}{2}$[f(x1)+f(x2)-f ( $\frac{{x}_{1}{+x}_{2}}{2}$)
=$\frac{1}{2}$[x12+(4-2a)x1+a2+1+x22+(4-2a)x2+a2+1]-[$\frac{{{(x}_{1}{+x}_{2})}^{2}}{4}$+$\frac{1}{2}$(4-2a)(x1+x2)+a2+1]
=$\frac{{{(x}_{1}{-x}_{2})}^{2}}{4}$>0,
∴P>Q.
(3)设存在这样的a,
由于0≤a≤8,∴-2≤a-2≤6,
①若-2≤a-2<0,即0≤a<2,则f(x)在[0,4]上为增函数,
∴f(0)=a2+1=7,解得:a=$\sqrt{3}$;
②若0≤a-2≤4,即2≤a≤6,
则f(a-2)=(a-2)2+(4-2a)(a-2)+a2+1=7,
化简得4a-11=0,解得 a=$\frac{11}{4}$,
综上,存在a=-1满足条件,
③若4<a-2≤6,即6<a≤8,则f(x)在[0,4]为减函数,
∴f(4)=16+4(4-2a)+a2+1=7,无解,
综上,存在实数a=$\sqrt{3}$或$\frac{11}{4}$∈[0,8],使得函数f(x)在[0,4]上的最小值为7.
点评 本题考查了二次函数的性质,考查函数的奇偶性、单调性问题,考查分类讨论思想,熟练掌握二次函数的性质是解题的关键,本题是一道中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{3}{4}$ | B. | $-\frac{{\sqrt{3}}}{4}$ | C. | $-\frac{3}{2}$ | D. | $-\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
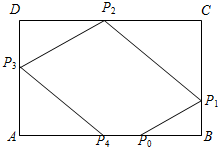 如图,矩形ABCD中,AB=3,AD=2,一质点从AB边上的点P0出发,沿与AB的夹角为θ的方向射到边BC上点P1后,依次反射(入射角与反射角相等)到边CD,DA和AB上的P2,P3,P4处.
如图,矩形ABCD中,AB=3,AD=2,一质点从AB边上的点P0出发,沿与AB的夹角为θ的方向射到边BC上点P1后,依次反射(入射角与反射角相等)到边CD,DA和AB上的P2,P3,P4处.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
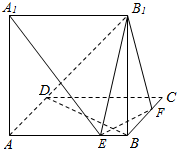 如图,正方形ABCD所在平面与正方形ABB1A1所在的平面垂直,且AB等于1.设E、F分别为AB、BC上的动点,(不包括端点)
如图,正方形ABCD所在平面与正方形ABB1A1所在的平面垂直,且AB等于1.设E、F分别为AB、BC上的动点,(不包括端点)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com