
【题目】某公司为了解所经销商品的使用情况,随机问卷50名使用者,然后根据这50名的问卷评分数据,统计得到如图所示的频率布直方图,其统计数据分组区间为[40,50),[50,60),[60,70),[70,80),[80,90),[90,100].

(1)求频率分布直方图中a的值并估计这50名使用者问卷评分数据的中位数;
(2)从评分在[40,60)的问卷者中,随机抽取2人,求此2人评分都在[50,60)的概率.
【答案】(1)a=0.006;76; (2)![]()
【解析】
(1)根据频率分布直方图,由概率之和为1求解a,设中位数为m,根据中位数平分直方图的面积求解.
(2)由频率分布直方图,可知在[40,50)内的人数:0.004×10×50=2,在[50,60)内的人数:0.006×10×50=3.设在[40,50)内的2人分别为a1,a2,在[50,60)内的3人分别为B1,B2,B3,列举出[40,60)的问卷者中随机抽取2人,基本事件的种数,再找出其中2人评分都在[50,60)内的基本事件的种数,利用古典概型的概率公式求解.
(1)由频率分布直方图,可得(0.004+a+0.0156+0.0232+0.0232+0.028)×10=1,
解得a=0.006.
由频率分布直方图,可设中位数为m,则有(0.004+0.006+0.0232)×10+(m﹣70)×0.028=0.5,解得中位数m=76.
(2)由频率分布直方图,可知在[40,50)内的人数:0.004×10×50=2,
在[50,60)内的人数:0.006×10×50=3.
设在[40,50)内的2人分别为a1,a2,在[50,60)内的3人分别为B1,B2,B3,
则从[40,60)的问卷者中随机抽取2人,基本事件有10种,分别为:
(a1,a2),(a1,B1),(a1,B2),(a1,B3),(a2,B1),
(a2,B2),(a2,B3),(B1,B2),(B1,B3),(B2,B3),
其中2人评分都在[50,60)内的基本事件有(B1,B2),(B1,B3),(B2,B3)共3种,
故此2人评分都在[50,60)的概率为![]() .
.


 应用题作业本系列答案
应用题作业本系列答案科目:高中数学 来源: 题型:
【题目】给定函数![]() 和
和![]() ,若存在常数
,若存在常数![]() ,
,![]() ,使得函数
,使得函数![]() 和
和![]() 对其公共定义域
对其公共定义域![]() 的任何实数
的任何实数![]() 分别满足
分别满足![]() 和
和![]() ,则称直线
,则称直线![]() :
:![]() 为函数
为函数![]() 和
和![]() 的“隔离直线”,给出下列四组函数:
的“隔离直线”,给出下列四组函数:
(1)![]() ,
,![]() ; (2)
; (2)![]() ,
,![]() ;
;
(3)![]() ,
,![]() ; (4)
; (4)![]() ,
,![]() ;
;
其中函数![]() 和
和![]() 存在“隔离直线”的序号是( )
存在“隔离直线”的序号是( )
A.(1)(3)B.(1)(3)(4)C.(1)(2)(3)D.(2)(4)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左右焦点分别为F1,F2,离心率为
的左右焦点分别为F1,F2,离心率为![]() ,设过点F2的直线l被椭圆C截得的线段为MN,当l⊥x轴时,|MN|=3.
,设过点F2的直线l被椭圆C截得的线段为MN,当l⊥x轴时,|MN|=3.
(1)求椭圆C的标准方程;
(2)在x轴上是否存在一点P,使得当l变化时,总有PM与PN所在的直线关于x轴对称?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 是衡量空气污染程度的一个指标,为了了解
是衡量空气污染程度的一个指标,为了了解![]() 市空气质量情况,从
市空气质量情况,从![]() 年每天的
年每天的![]() 值的数据中随机抽取
值的数据中随机抽取![]() 天的数据,其频率分布直方图如图所示.将
天的数据,其频率分布直方图如图所示.将![]() 值划分成区间
值划分成区间![]() 、
、![]() 、
、![]() 、
、![]() ,分别称为一级、二级、三级和四级,统计时用频率估计概率 .
,分别称为一级、二级、三级和四级,统计时用频率估计概率 .
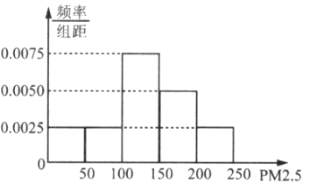
(1)根据![]() 年的数据估计该市在
年的数据估计该市在![]() 年中空气质量为一级的天数;
年中空气质量为一级的天数;
(2)按照分层抽样的方法,从样本二级、三级、四级中抽取![]() 天的
天的![]() 数据,再从这
数据,再从这![]() 个数据中随机抽取
个数据中随机抽取![]() 个,求仅有二级天气的概率.
个,求仅有二级天气的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着生活节奏的加快以及智能手机的普及,外卖点餐逐渐成为越来越多用户的餐饮消费习惯.由此催生了一批外卖点餐平台,已知某外卖平台的送餐费用与送餐距离有关(该平台只给5千米范围内配送),为调査送餐员的送餐收入,现从该平台随机抽取80名点外卖的用户进行统计,按送餐距离分类统计结果如下表:

以这80名用户送餐距离位于各区间的频率代替送餐距离位于该区间的概率.
(1)从这80名点外卖的用户中任取一名用户.求该用户的送餐距离不超过3千米的概率;
(2)试估计利用该平台点外卖用户的平均送餐距离;
(3)若该外卖平台给送餐员的送餐贽用与送餐距离有关,规定2千米内为短距离,每份3元,2千米到4千米为中距离,每份5元;超过4千米为远距离,每份9元,若送餐员一天的目标收 人不低于150元,试估计一天至少要送多少份外卖?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是线段
是线段![]() 上靠近点
上靠近点![]() 的一个三等分点,点
的一个三等分点,点![]() 是线段
是线段![]() 上的一个动点,且
上的一个动点,且![]() .如图,将
.如图,将![]() 沿
沿![]() 折起至
折起至![]() ,使得平面
,使得平面![]() 平面
平面![]() .
.
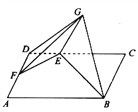
(1)当![]() 时,求证:
时,求证:![]() ;
;
(2)是否存在![]() ,使得
,使得![]() 与平面
与平面![]() 所成的角的正弦值为
所成的角的正弦值为![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() ,
,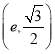 在椭圆
在椭圆![]() 上,其中
上,其中![]() 为椭圆的离心率.
为椭圆的离心率.
(1)求椭圆![]() 的方程;
的方程;
(2)直线![]() 经过
经过![]() 的上顶点且
的上顶点且![]() 与抛物线
与抛物线![]() 交于
交于![]() ,
,![]() 两点,
两点,![]() 为椭圆的焦点,直线
为椭圆的焦点,直线![]() ,
,![]() 与
与![]() 分别交于点
分别交于点![]() (异于点
(异于点![]() ),
),![]() (异于点
(异于点![]() ),证明:直线
),证明:直线![]() 的斜率为定值.
的斜率为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com