练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图所示是一个上下底面均是边长为2的正三角形的直三棱柱,且该直三棱柱的高为4,D为AB的中点,E为CC1的中点.

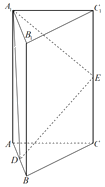
    （1）求DE与平面ABC夹角的正弦值;

    （2）求二面角A﹣A1D﹣E的余弦值.

    【答案】（1）.（2）

    【解析】

    （1）如图所示,建立空间直角坐标系.利用向量法求DE与平面ABC夹角的正弦值;（2）利用向量法求二面角A﹣A1D﹣E的余弦值.

    （1）如图所示,建立空间直角坐标系.

    D(,,0),E(0,2,2),,,2),

    平面ABC的法向量为(0,0,1).

    ∴DE与平面ABC夹角的正弦值=|cos,|.

    （2）设平面A1DE的法向量为(x,y,z),由0,可得y+2z=0,2y﹣2z=0,

    取(7,,).

    同理可得平面AA1D的法向量,,0),

    ∴cos,.

    ∴二面角A﹣A1D﹣E的余弦值为.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】在数列中，已知.

    （1）求数列的通项公式；

    （2）求证：数列是等差数列；

    （3）设数列满足的前项和.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某中学高三年级有学生500人，其中男生300人，女生200人。为了研究学生的数学成绩是否与性别有关，采用分层抽样的方法，从中抽取了100名学生，统计了他们期中考试的数学分数，然后按照性别分为男、女两组，再将两组的分数分成5组： 分别加以统计，得到如图所示的频率分布直方图。

    （I）从样本分数小于110分的学生中随机抽取2人，求两人恰为一男一女的概率；

    （II）若规定分数不小于130分的学生为“数学尖子生”，请你根据已知条件完成2×2列联表，并判断是否有90%的把握认为“数学尖子生与性别有关”?

    附表：

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，.

    （1）求函数在上的最大值；

    （2）若函数在区间上有零点，求的取值范围；

    （3）求证：.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】将正方体ABCD﹣A1B1C1D1沿三角形A1BC1所在平面削去一角可得到如图所示的几何体.

    （1）连结BD,BD1,证明:平面BDD1⊥平面A1BC1;

    （2）已知P,Q,R分别是正方形ABCDCDD1C1ADD1A1的中心(即对角线交点),证明:平面PQR∥平面A1BC1.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示，在四棱锥中，底面为正方形.且，，.

    （1）证明：平面；

    （2）求二面角的余弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，，.

    （1）若，.

    ①当时，证明：；

    ②若有两个不相等的零点，且，证明：；

    （2）讨论的单调性.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，，

    （1）当时，求的最大值和最小值；

    （2）求实数的取值范围，使在区间上是单调函数.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】一片森林原来面积为，计划每年砍伐一些树，且每年砍伐面积的百分比相等，当砍伐到面积的一半时，所用时间是10年，为保护生态环境，森林面积至少要保留原面积的，已知到今年为止，森林剩余面积为原来的.

    （1）到今年为止，该森林已砍伐了多少年？

    （2）今后最多还能砍伐多少年？

    查看答案和解析>>

    同步练习册答案