
【题目】给出下列四个命题:
①函数![]() 的图像过定点
的图像过定点![]() ;
;
②已知函数![]() 是定义在
是定义在![]() 上的偶函数,当
上的偶函数,当![]() 时,
时,![]() ,则
,则![]() 的解析式为
的解析式为![]() ;
;
③函数![]() 的图像可由函数
的图像可由函数![]() 图像向右平移一个单位得到;
图像向右平移一个单位得到;
④函数![]() 图像上的点到
图像上的点到![]() 距离的最小值是
距离的最小值是![]() .
.
其中所有正确命题的序号是_____________.
科目:高中数学 来源: 题型:
【题目】已知关于![]() 的方程为
的方程为![]() .
.
(Ⅰ)若![]() ,
,![]() ,求方程有实数根的概率.
,求方程有实数根的概率.
(Ⅱ)若![]() ,
,![]() ,求方程有实数根的概率.
,求方程有实数根的概率.
(Ⅲ)在区间![]() 上任取两个数
上任取两个数![]() 和
和![]() ,利用随机数模拟的方法近似计算关于
,利用随机数模拟的方法近似计算关于![]() 的方程
的方程![]() 有实数根的概率,请写出你的试验方法.
有实数根的概率,请写出你的试验方法.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】光线通过一块玻璃,其强度要损失10%,把几块这样的玻璃重叠起来,设光线原来的强度为![]() ,通过
,通过![]() 块玻璃以后强度为
块玻璃以后强度为![]() .
.
(Ⅰ)写出![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(Ⅱ)通过多少块玻璃以后,光线强度减弱到原来的![]() 以下.(lg3≈0.4771).
以下.(lg3≈0.4771).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某研究性学习小组对春季昼夜温差大小与某花卉种子发芽多少之间的关系进行研究,他们分别记录了3月1日至3月5日的每天昼夜温差与实验室每天每100颗种子浸泡后的发芽数,得到如下资料:

(1)从3月1日至3月5日中任选2天,记发芽的种子数分别为![]() ,求事件“
,求事件“![]() 均小于25”的概率;
均小于25”的概率;
(2)请根据3月2日至3月4日的数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() .
.
(参考公式:回归直线方程为![]() ,其中
,其中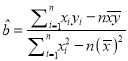 ,
, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知关于某设备的使用年限![]() 与所支出的维修费用
与所支出的维修费用![]() (万元),有如下统计资料:
(万元),有如下统计资料:
设![]() 对
对![]() 呈线性相关关系,试求:
呈线性相关关系,试求:

(1)线性回归方程![]() 的回归系数
的回归系数![]() ;
;
(2)估计使用年限为10年时,维修费用是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知甲、乙两地相距为![]() 千米,汽车从甲地匀速行驶到乙地,速度每小时不超过
千米,汽车从甲地匀速行驶到乙地,速度每小时不超过![]() 千米.已知汽车每小时的运输成本(单位:元)由可变部分和固定部分组成:固定部分为
千米.已知汽车每小时的运输成本(单位:元)由可变部分和固定部分组成:固定部分为![]() 元,可变部分与速度
元,可变部分与速度![]() (单位;
(单位; ![]() )的平方成正比,且比例系数为
)的平方成正比,且比例系数为![]() .
.
(1)求汽车全程的运输成本![]() (单位:元)关于速度
(单位:元)关于速度![]() (单位;
(单位; ![]() )的函数解析式;
)的函数解析式;
(2)为了全程的运输成本最小,汽车应该以多大的速度行驶?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com