
【题目】设f(x)是定义在R上的奇函数,且当x≥0时, ![]() ,若存在x∈[t2﹣1,t],使不等式f(2x+t)≥2f(x)成立,则实数t的取值范围是. .
,若存在x∈[t2﹣1,t],使不等式f(2x+t)≥2f(x)成立,则实数t的取值范围是. .
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:高中数学 来源: 题型:
【题目】如图所示,正三角形ABC所在平面与梯形BCDE所在平面垂直,![]() ,
,![]() =4 ,
=4 ,![]() ,F为棱AE的中点.
,F为棱AE的中点.

(1)求证:平面![]() 平面
平面![]() ;
;
(2)若直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某教师有相同的语文参考书3本,相同的数学参考书4本,从中取出4本赠送给4位学生,每位学生1本,则不同的赠送方法共有( )
A. 15种 B. 20种 C. 48种 D. 60种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在探究实系数一元二次方程的根与系数的关系时,可按下述方法进行:
设实系数一元二次方程![]() ……①
……①
在复数集![]() 内的根为
内的根为![]() ,
, ![]() ,则方程①可变形为
,则方程①可变形为![]() ,
,
展开得![]() .……②
.……②
比较①②可以得到: 
类比上述方法,设实系数一元![]() 次方程
次方程![]() (
(![]() 且
且![]() )在复数集
)在复数集![]() 内的根为
内的根为![]() ,
, ![]() ,…,
,…, ![]() ,则这
,则这![]() 个根的积
个根的积![]() __________.
__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学在研究函数f(x)= ![]() ﹣1(x∈R)时,得出了下面4个结论:①等式f(﹣x)=f(x)在x∈R时恒成立;②函数f(x)在x∈R上的值域为(﹣1,1];③曲线y=f(x)与g(x)=2x﹣2仅有一个公共点;④若f(x)=
﹣1(x∈R)时,得出了下面4个结论:①等式f(﹣x)=f(x)在x∈R时恒成立;②函数f(x)在x∈R上的值域为(﹣1,1];③曲线y=f(x)与g(x)=2x﹣2仅有一个公共点;④若f(x)= ![]() ﹣1在区间[a,b](a,b为整数)上的值域是[0,1],则满足条件的整数数对(a,b)共有5对.其中正确结论的序号有(请将你认为正确的结论的序号都填上).
﹣1在区间[a,b](a,b为整数)上的值域是[0,1],则满足条件的整数数对(a,b)共有5对.其中正确结论的序号有(请将你认为正确的结论的序号都填上).
查看答案和解析>>
科目:高中数学 来源: 题型:
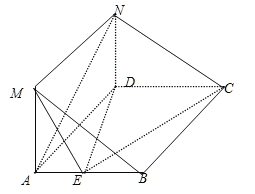
【题目】在如图所示的几何体中,平面![]() 平面
平面![]() ,四边形
,四边形![]() 是菱形,四边形
是菱形,四边形![]() 是矩形,
是矩形,![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 的中点.
的中点.
(Ⅰ)求证:![]() 平面
平面![]() ;
;
(II)在线段![]() 上是否存在点
上是否存在点![]() ,使二面角
,使二面角![]() 的大小为
的大小为![]() ?若存在,求出
?若存在,求出![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com