
(1)已知命题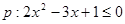 和命题
和命题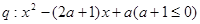 ,若
,若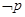 是
是 的必要不充分条件,求实数
的必要不充分条件,求实数 的取值范围.
的取值范围.
(2)已知命题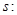 方程
方程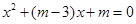 的一根在
的一根在 内,另一根在
内,另一根在 内.
内.
命题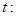 函数
函数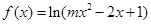 的定义域为全体实数.
的定义域为全体实数.
若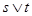 为真命题,求实数
为真命题,求实数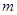 的取值范围.
的取值范围.
(1)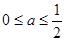 (2)
(2)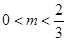 或
或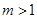
解析试题分析:(1)解决命题问题,首先要转化为相应的数学问题进行解答,然后再利用命题的逻辑关系列式求解.先解二次不等式,求出两个命题对应的范围,然后利用集合关系判断充要条件的方法列不等式组求解;判断充要条件要注意“方向性”.(2)二次方程在区间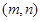 内的实数根判定,要结合二次函数图像的特征考虑三个条件:判别式的符号、对称轴与区间的位置关系、区间端点的函数值的符号.先利用判断二次方程的根、二次不等式的解集为
内的实数根判定,要结合二次函数图像的特征考虑三个条件:判别式的符号、对称轴与区间的位置关系、区间端点的函数值的符号.先利用判断二次方程的根、二次不等式的解集为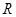 的条件,求出两个命题对应的范围,然后利用“或”命题为真命题列不等式组求解.
的条件,求出两个命题对应的范围,然后利用“或”命题为真命题列不等式组求解.
试题解析:(1)对于命题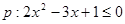 ,解得:
,解得: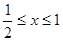 1分
1分
对于命题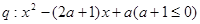 ,解得:
,解得: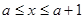 3分
3分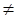 由
由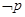 是
是 的必要不充分条件,所以
的必要不充分条件,所以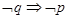 且
且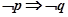 .
.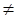 于是所以
于是所以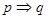 且
且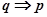 . 5分
. 5分
所以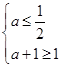 .解得
.解得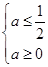 ,即:
,即: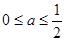
所以实数 的取值范围是
的取值范围是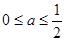 7分
7分
(2)对于命题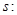 方程
方程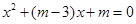 的一根在
的一根在 内,另一根在
内,另一根在 内,
内,
设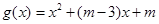 ,则:
,则: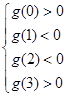 ,即:
,即: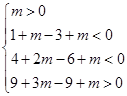 9分
9分
解得: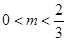 10分
10分
对于命题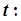 函数
函数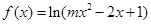 的定义域为全体实数,
的定义域为全体实数,
则有: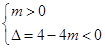 12分
12分
解得: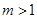 13分
13分
又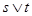 为真命题,即
为真命题,即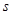 为真命题或
为真命题或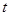 为真命题。
为真命题。
所以所求实数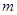 的取值范围为
的取值范围为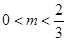 或
或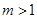 . 14分
. 14分
考点:1.命题真假的判定 2.充要条件的判定 3.二次方程实数根的判定


 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com