
分析 设向量$\overrightarrow a$,$\overrightarrow b$的夹角为θ,根据平面向量的数量积与夹角公式计算即可.
解答 解:设向量$\overrightarrow a$,$\overrightarrow b$的夹角为θ,则θ∈[0°,180°];
又$\overrightarrow{a}$•($\overrightarrow{a}$+$\overrightarrow{b}$)=0,2|$\overrightarrow{a}$|=|$\overrightarrow{b}$|,
∴${\overrightarrow{a}}^{2}$+$\overrightarrow{a}$•$\overrightarrow{b}$=0,
即${|\overrightarrow{a}|}^{2}$+|$\overrightarrow{a}$|×2|$\overrightarrow{a}$|cosθ=0,
解得cosθ=-$\frac{1}{2}$,
∴θ=120°,
即向量$\overrightarrow a$,$\overrightarrow b$夹角为120°.
故答案为:120°.
点评 本题考查了平面向量的数量积与夹角公式的应用问题,是基础题.


科目:高中数学 来源: 题型:选择题
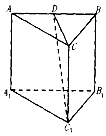
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 144种 | B. | 288种 | C. | 360种 | D. | 720种 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
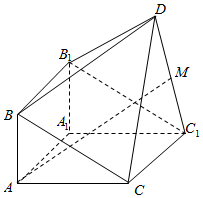 如图,由直三棱柱ABC-A1B1C1和四棱锥D-BB1C1C构成的几何体中,∠BAC=90°,AB=1,BC=BB1=2,C1D=CD=$\sqrt{5}$,平面CC1D⊥平面ACC1A1.
如图,由直三棱柱ABC-A1B1C1和四棱锥D-BB1C1C构成的几何体中,∠BAC=90°,AB=1,BC=BB1=2,C1D=CD=$\sqrt{5}$,平面CC1D⊥平面ACC1A1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 400π | B. | 300π | C. | 200π | D. | 100π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | c<b<a | B. | a<b<c | C. | c<a<b | D. | b<a<c |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com