
【题目】《厉害了,我的国》这部电影记录:到2017年底,我国高铁营运里程达2.5万公里,位居世界第一位,超过第二名至第十名的总和,约占世界高铁总量的三分之二.如图是我国2009年至2017年高铁营运里程(单位:万公里)的折线图.

根据这9年的高铁营运里程,甲、乙两位同学分别选择了![]() 与时间变量
与时间变量![]() 的两个回归模型①:
的两个回归模型①:![]() ;②
;②![]() .
.
(1)求![]() ,
,![]() (精确到0.01);
(精确到0.01);
(2)乙求得模型②的回归方程为![]() ,你认为哪个模型的拟合效果更好?并说明理由.
,你认为哪个模型的拟合效果更好?并说明理由.
附:参考公式: ,
,![]() ,
,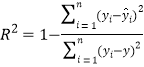 .
.
参考数据:
|
|
|
|
|
|
1.39 | 76.94 | 285 | 0.22 | 0.09 | 3.72 |
科目:高中数学 来源: 题型:
【题目】为了鼓励市民节约用电,实行“阶梯式”电价,某边远山区每户居民月用电量划分为三档:月用电量不超过150度,按0.6元/度收费,超过150度但不超过250度的部分每度加价0.1元,超过250度的部分每度再加价0.3元收费.
(1)求该边远山区某户居民月用电费用![]() (单位:元)关于月用电量
(单位:元)关于月用电量![]() (单位:度)的函数解析式;
(单位:度)的函数解析式;
(2)已知该边远山区贫困户的月用电量![]() (单位:度)与该户长期居住的人口数
(单位:度)与该户长期居住的人口数![]() (单位:人)间近似地满足线性相关关系:
(单位:人)间近似地满足线性相关关系:![]() (
(![]() 的值精确到整数),其数据如表:
的值精确到整数),其数据如表:
| 14 | 15 | 17 | 18 |
| 161 | 168 | 191 | 200 |
现政府为减轻贫困家庭的经济负担,计划对该边远山区的贫困家庭进行一定的经济补偿,给出两种补偿方案供选择:一是根据该家庭人数,每人每户月补偿6元;二是根据用电量每人每月补偿![]() (
(![]() 为用电量)元,请根据家庭人数
为用电量)元,请根据家庭人数![]() 分析,一个贫困家庭选择哪种补偿方式可以获得更多的补偿?
分析,一个贫困家庭选择哪种补偿方式可以获得更多的补偿?
附:回归直线![]() 中斜率和截距的最小二乘法估计公式分别为:
中斜率和截距的最小二乘法估计公式分别为:
 ,
,![]() .
.
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在等差数列{an}中,2a9=a12+13,a3=7,其前n项和为Sn.
(1)求数列{an}的通项公式;
(2)求数列{![]() }的前n项和Tn,并证明Tn<
}的前n项和Tn,并证明Tn<![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,设S为△ABC的面积,满足S=![]() (a2+c2﹣b2).
(a2+c2﹣b2).
(1)求角B的大小;
(2)若边b=![]() ,求a+c的取值范围.
,求a+c的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是函数![]() 的导函数
的导函数![]() 的图象,给出下列命题:
的图象,给出下列命题:

①-2是函数![]() 的极值点;
的极值点;
②![]() 是函数
是函数![]() 的极值点;
的极值点;
③![]() 在
在![]() 处取得极大值;
处取得极大值;
④函数![]() 在区间
在区间![]() 上单调递增.则正确命题的序号是
上单调递增.则正确命题的序号是
A. ①③ B. ②④ C. ②③ D. ①④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,将从点M出发沿纵、横方向到达点N的任一路径称为M到N的一条“L路径”.如图所示的路径MM1M2M3N与路径MN1N都是M到N的“L路径”.某地有三个新建居民区,分别位于平面xOy内三点A(3,20),B(﹣10,0),C(14,0)处.现计划在x轴上方区域(包含x轴)内的某一点P处修建一个文化中心.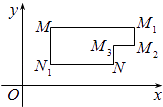
(1)写出点P到居民区A的“L路径”长度最小值的表达式(不要求证明);
(2)若以原点O为圆心,半径为1的圆的内部是保护区,“L路径”不能进入保护区,请确定点P的位置,使其到三个居民区的“L路径”长度之和最小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com