
【题目】给定直线m:y=2x-16,抛物线C:y2=ax(a>0).
(1)当抛物线C的焦点在直线m上时,确定抛物线C的方程;
(2)若△ABC的三个顶点都在(1)所确定的抛物线C上,且点A的纵坐标y=8,△ABC的重心恰在抛物线C的焦点上,求直线BC的方程.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
试题(1)由抛物线的标准方程可得其焦点为![]() ,它在直线
,它在直线![]() 上,代入可得
上,代入可得![]() 值;(2)由已知
值;(2)由已知![]() 点坐标为
点坐标为![]() ,焦点为
,焦点为![]() ,因此由重心坐标公式得
,因此由重心坐标公式得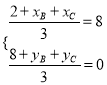 ,从而有
,从而有![]() ,故得出
,故得出![]() 中点坐标为
中点坐标为![]() ,
,![]() 的斜率求法是:把坐标
的斜率求法是:把坐标![]() 代入抛物线方程,所得两式相减(点差法)可得
代入抛物线方程,所得两式相减(点差法)可得![]() .
.
试题解析:(1)∵抛物线的焦点为(![]() ,0),代入y=2x-16,得a=32.
,0),代入y=2x-16,得a=32.
∴抛物线方程为y2=32x.
(2)∵yA=8,∴xA=2.
∵F(8,0)为△ABC的重心,∴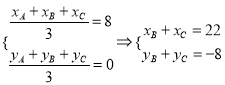
又![]() (yB+yC)(yB-yC)=32(xB-xC)
(yB+yC)(yB-yC)=32(xB-xC)![]()
![]()
![]() =-4=kBC,
=-4=kBC,
又中线AF与BC交点坐标x=![]() =11,y=
=11,y=![]() =
=![]() =-4,
=-4,
∴BC的直线方程为y+4=-4(x-11),即4x+y-40=0.


 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() 分别为双曲线
分别为双曲线![]()
![]()
![]() 的左、右焦点,点P是以
的左、右焦点,点P是以![]() 为直径的圆与C在第一象限内的交点,若线段
为直径的圆与C在第一象限内的交点,若线段![]() 的中点Q在C的渐近线上,则C的两条渐近线方程为__________.
的中点Q在C的渐近线上,则C的两条渐近线方程为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给定椭圆![]() .称圆心在原点O,半径为
.称圆心在原点O,半径为![]() 的圆是椭圆C的“准圆”.若椭圆C的一个焦点为
的圆是椭圆C的“准圆”.若椭圆C的一个焦点为![]() ,其短轴上的一个端点到F的距离为
,其短轴上的一个端点到F的距离为![]() .
.
(1)求椭圆C的方程和其“准圆”方程;
(2)点P是椭圆C的“准圆”上的一个动点,过动点P作直线![]() ,使得
,使得![]() 与椭圆C都只有一个交点,试判断
与椭圆C都只有一个交点,试判断![]() 是否垂直?并说明理由.
是否垂直?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() )以坐标原点为极点,
)以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设曲线![]() 和
和![]() 交于
交于![]() ,
,![]() 两点,点
两点,点![]() ,若
,若![]() ,
,![]() ,
,![]() 成等比数列,求
成等比数列,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A.若![]() 为真命题,则
为真命题,则![]() ,
,![]() 均为假命题;
均为假命题;
B.命题“若![]() ,则
,则![]() ”的逆否命题为真命题;
”的逆否命题为真命题;
C.等比数列![]() 的前
的前![]() 项和为
项和为![]() ,若“
,若“![]() ”则“
”则“![]() ”的否命题为真命题;
”的否命题为真命题;
D.“平面向量![]() 与
与![]() 的夹角为钝角”的充要条件是“
的夹角为钝角”的充要条件是“![]() ”
”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在第十五次全国国民阅读调查中,某地区调查组获得一个容量为![]() 的样本,其中城镇居民
的样本,其中城镇居民![]() 人,农村居民
人,农村居民![]() 人.在这些居民中,经常阅读的城镇居民
人.在这些居民中,经常阅读的城镇居民![]() 人,农村居民
人,农村居民![]() 人.
人.
(1)填写下面列联表,并判断是否有![]() 的把握认为,经常阅读与居民居住地有关?
的把握认为,经常阅读与居民居住地有关?
城镇居民 | 农村居民 | 合计 | |
经常阅读 |
|
| |
不经常阅读 | |||
合计 |
|
(2)调查组从该样本的城镇居民中按分层抽样抽取出![]() 人,参加一次阅读交流活动,若活动主办方从这
人,参加一次阅读交流活动,若活动主办方从这![]() 位居民中随机选取
位居民中随机选取![]() 人作交流发言,求被选中的
人作交流发言,求被选中的![]() 位居民都是经常阅读居民的概率.
位居民都是经常阅读居民的概率.
附:![]() ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD是边长为1的正方形,MD⊥ABCD,NB⊥ABCD.且MD=NB=1.则下列结论中:
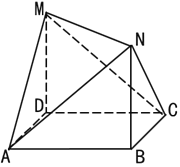
①MC⊥AN
②DB∥平面AMN
③平面CMN⊥平面AMN
④平面DCM∥平面ABN
所有假命题的个数是( )
A.0B.1C.2D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,《宋人扑枣图轴》是作于宋朝的中国古画,现收藏于中国台北故宫博物院.该作品简介:院角的枣树结实累累,小孩群来攀扯,枝桠不停晃动,粒粒枣子摇落满地,有的牵起衣角,有的捧着盘子拾取,又玩又吃,一片兴高采烈之情,跃然于绢素之上.甲、乙、丙、丁四人想根据该图编排一个舞蹈,舞蹈中他们要模仿该图中小孩扑枣的爬、扶、捡、顶四个动作,四人每人模仿一个动作.若他们采用抽签的方式来决定谁模仿哪个动作,则甲不模仿“爬”且乙不模仿“扶”的概率是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com